Cascading Hydro Networks

Contents

  1. Introduction
  2. The Potential Energy Model
  3. Hydro Generator Efficiency
  4. The Level Model
  5. The Volume Model
  6. Hydraulic Connections in a Cascade
  7. Hydro Visualization Tools

1. Introduction

The previous chapters of this article dealt with 'stand alone' storages or simple 'closed circuit' pumped storage systems. In those systems the conversion of water to electrical energy is a static function and thus storage volumes can be expressed in units of potential energy (GWh)

2. The Potential Energy Model

When one considers a cascade of storages with multiple generators, however, the potential energy in the system is not simply a function of the total volume of water in the system, but also of which storages are holding that water. Consider a system with two storages and identical generators in a linear cascade like Figure 1. On the left the upper storage is full, the lower is empty and vice versa on the right. The potential energy in the left-hand system is double that of the right-hand system. This is because water stored in the upper storage can generate in both the upper and lower generators, whereas water in the lower storage can only generate in the lower generator.

Figure 1: Simple cascade


Again if this system remains "static" it can still be modelled in PLEXOS as a potential energy network. All that is required is to express the volume of the upper storage in terms of potential energy for the entire cascade, and then apply a scaling factor that "derates" that potential energy once it passes through the upper generator.

In fact hydro efficiency can vary even in a single storage model due to head effects: efficiency varies as a function of the difference in heights of the head and tail storages which varies as those storages are filled/emptied.

once it passes through the upper generator. PLEXOS provides the properties Generator Head Storage Flow Factor and Generator Tail Storage Flow Factor for just this purpose.

However if at any time one of the generators in the cascade goes out-of-service the simplistic scaling of potential energy will not be accurate. Further, if the cascade is anything but a linear system, e.g. if multiple sources feed a storage, then again the potential energy model is not accurate. Thus PLEXOS provides alternate hydro models that work on raw volumes of water for storage and directly model generator efficiency.

3. Hydro Generator Efficiency

In the Level and Volume models in metric mode, hydro generator efficiency is expressed in megawatts per cubic meter second (MW/cumec) i.e. it is the rate of production that results from a flow rate through the turbine of one cubic meter per second. This efficiency is input via the property Generator Efficiency Incr.

Hydro generator efficiency is allowed to vary according to the generation level by using Efficiency Incr in multiple bands with Load Point, usually in combination with the "intercept" term Efficiency Base. An example is shown in Figure 2 (in metric units).

PLEXOS develops a piecewise-linear approximation to the efficiency function, and this is illustrated in Figure 2 (showing flow rates) and Figure 3 (showing volumes of water through the turbine per hour).

Table 1: Hydro efficiency curve (metric)
Property Value Units Band
Units 1 - -
Max Capacity 60 MW -
Load Point 20 MW 1
Load Point 40 MW 2
Load Point 60 MW 3
Efficiency Base 58 cumec -
Efficiency Incr 0.5 MW/cumec 1
Efficiency Incr 0.48 MW/cumec 2
Efficiency Incr 0.42 MW/cumec 3
Table 2: Hydro efficiency curve (imperial US)
Property Value Units Band
Units 1 - -
Max Capacity 60 MW -
Load Point 20 MW 1
Load Point 40 MW 2
Load Point 60 MW 3
Efficiency Base 58 cumec -
Efficiency Incr 0.5 MW/cumec 1
Efficiency Incr 0.48 MW/cumec 2
Efficiency Incr 0.42 MW/cumec 3

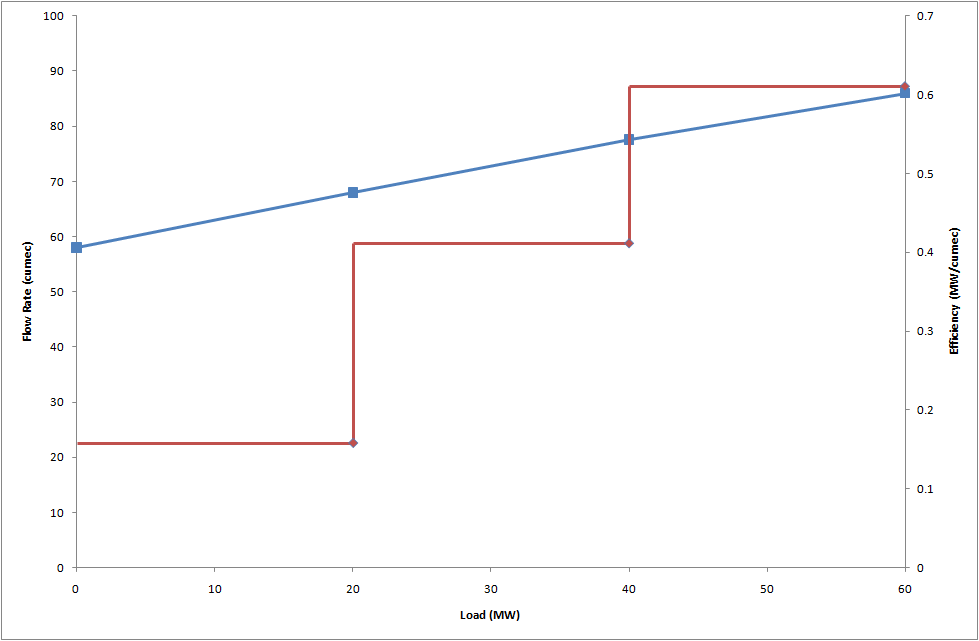
Figure 2: Generator efficiency - flow rate and piecewise linear incremental efficiency (metric units)
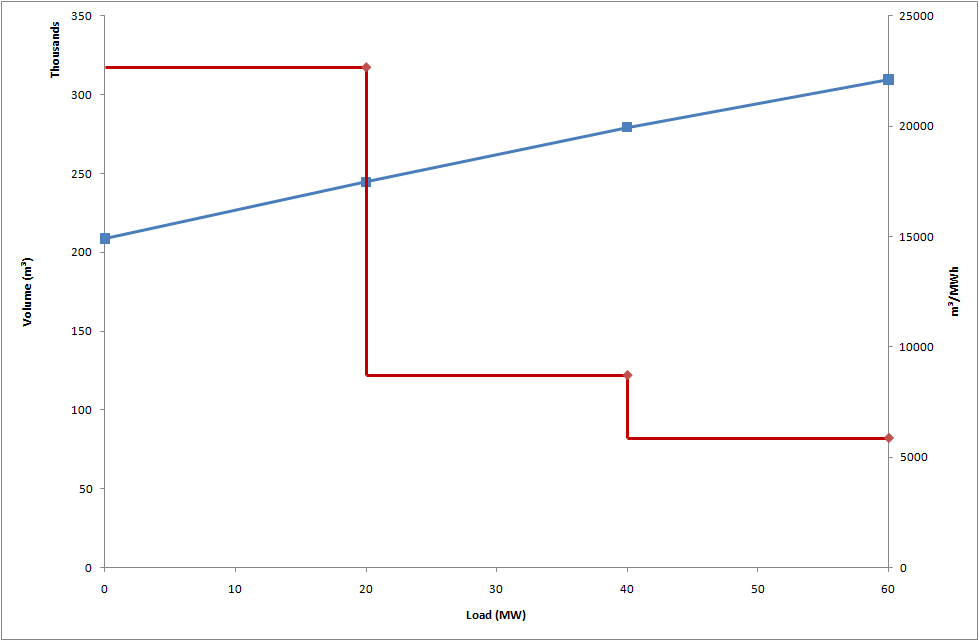
Figure 3: Generator efficiency - water volume and piecewise linear incremental efficiency (metric units)

4. The Level Model

Storages in the Level Model define their capacity using two pairs of elevation and area measures expressed as these Storage properties:

It is important to note that these pairs are only used to define the storage shape as illustrated in Figure 4. The additional properties Min Level and Max Level define the feasible range of storage levels allowed: these need not be within the Low Ref Level and High Ref Level range. If preferred these limits can be defined using Min Volume and Max Volume where zero volume is defined at the Low Ref Level.

Figure 4: Level Model parameters

PLEXOS converts the level information to volumes for use in the storage optimization and in interpreting and reporting volume-based limits and solution values. Given the reference pairs, the volume in the storage v equivalent to a given level h is computed using the formula:

and:

h is the Storage Min Level (minimum defined in entire horizon)
a* and a* are the Storage Low Ref Area and High Ref Area respectively
h* and h* are the Storage Low Ref Level and High Ref Level respectively

The volume in storage v can be then converted back to level h by "completing the square":

Case 7

Storage using the level model:

As a demonstration of the Level model and use of hydro generator efficiency, assume we wish to convert the hydro generator with storage in our example developed earlier (Case 3) to one of the same 'size', in terms of potential energy, but defined using level data. For simplicity assume that:

  • the storage has straight sides (a=a) and that it has an elevation of 100m when full, zero when empty (h=0,h=100). This means that the total volume in storage is given by v=100•a.
  • hydro generator efficiency is constant at 1 MW/cumec

The potential energy in the storage is given by e=v/(3600=(100•-a)/3600). Solving for the required area given a requirement for 5000 GWh of potential gives:

a=(e•3600)/100=(5 000 000•3600)/100=180 000 000 m2

Note that the factor of 3600 converts the cumec flow rate into an equivalent hourly quantity. Also note the conversion of GWh to MWh. The corresponding Storage input to PLEXOS is shown in Table 3. We must also set Generator Efficiency Incr = 1 for this example.

Table 3: Storage input for Level model
Property Value Units
Min Level 0 m
Max Level 100 m
Initial Level 100 m
Low Ref Level 0 m
Low Ref Area 180, 000, 000 m3
High Ref Level 100 m
High Ref Area 180, 000, 000 m3

In the metric Level model Generator Efficiency is defined in units of MW/cumec rather than MWh/MWh implied by the potential energy model. In this example a generator efficiency of unity implies that megawatts and cumec are interchangeable thus we do not need to convert the existing Storage Natural Inflow data i.e. the same nominal values will 'work' as cumec.

The results for this case in terms of thermal production cost and energy prices are identical to Case 3 above. The reported storage results however are now in units reflecting volumes of water as in Table X.

Month Initial Volume
(1000 m3)		 Inflow
(1000 m3)		 Release
(1000m3)		 End Volume
(1000m3)		 End Level
(m)		 Shadow Price
($/1000m3)
Jan 18, 000, 000 1, 261, 526 1, 632, 981 17, 628, 545 98 35.7
Feb 17, 628, 545 1, 376, 525 1, 176, 178 17, 828, 892 99 35.85
Mar 17, 828, 892 1, 491, 869 1, 324, 077 17, 993, 731 100 35.83
Apr 17, 996, 684 1, 607, 040 1, 609, 993 17, 993, 731 100 36.41
May 17, 993, 731 1, 146, 355 1, 140, 086 18, 000, 000 100 45.54
Jun 18, 000, 000 572, 832 1, 212, 855 17, 359, 977 96 50.53
Jul 17, 359, 977 0 1, 416, 630 15, 943, 347 89 50.76
Aug 15, 943, 347 115, 171 1, 369, 490 14, 662, 881 81 51.1
Sep 14, 689, 028 1, 148, 256 1, 174, 403 14, 662, 881 81 49.32
Oct 14, 662, 881 1, 376, 698 705, 187 15, 334, 391 85 50.79
Nov 15, 334, 391 1, 721, 088 240, 416 16, 815, 063 93 50.79
Dec 16, 815, 063 1, 261, 526 76, 590 18, 000, 000 100 51.95

5. The Volume Model

Storages in the Volume Model define their capacity in units of water volume:

  • Cumec days (CMD) for the metric model;
  • Acre feet (AF) for the imperial model.

As discussed above, the central difference between the Level and the Volume model is the way storage dimensions are defined. The volume model uses the same flow units as the Level model.

Case 8

Storage using the volume model:

A cumec day is the volume of water released in a day at a rate of one cumec (cubic metre per second), thus 1 CMD = 3600 × 24 = 86400m3.

Thus to adapt the Level model example above, we need only divide the cubic metre figures by this amount. This gives the following set of Storage input:

Table 6: Results for Case 8
Property Value Units
Min Volume 0 CMD
Max Volume 208333 CMD
Initial Volume 208333 CMD

Storage inflows are in cumec (metric) or acre-feet per hour (imperial). For our example the existing cumec-based Storage Natural Inflow values remain unchanged.

Table 6: Results for Case 8
Month
 Initial Volume
(CMD)		 Inflow
(CMD)		 Release
(CMD)		 End Volume
(CMD)		 Shadow Price
($/CMD)
Jan 208, 333 14, 601 18, 900 204, 034 856.8
Feb 204, 034 15, 932 13, 613 206, 353 860, 46
Mar 206, 352 17, 267 15, 325 208, 261 873.82
Apr 208, 295 18, 600 18, 634 208, 261 873.82
May 208, 261 13, 268 13, 195 208, 333 1, 092.93
Jun 208, 333 6, 630 14, 038 200, 926 1, 212.81
Jul 200, 926 0 16, 396 184, 530 1, 218. 325
Aug 184, 530 1, 333 15, 851 170, 012 1, 226.47
Sep 170, 012 13, 290 13, 593 169, 709 1, 183.664
Oct 169, 709 15, 934 8, 162 177, 481 1, 222. 397
Nov 177, 481 19, 920 2, 783 194, 619 1, 218. 936
Dec 194, 619 14, 601 886 208, 333 1, 246.831

6. Hydraulic Connections in a Cascade

The building blocks of a cascading hydro network are:

  • Storage
  • Generator
  • Waterway
  • Initial Storage Position
  • Natural Inflows

Generators flow water from their Head Storage to their Tail Storage. Where the Tail Storage is not defined, the water flows 'to the sea'. Thus Generator objects are the primary mechanism for connecting Storage objects in a cascading network. Where a storage connects to one or more others without flowing water through a turbine use the Waterway class. A Waterway flows water from its Storage From to its Storage To. Again, when the Storage To is not defined, the waterway flows water 'to the sea' i.e. it is a 'spill'. The final element is natural inflows, which are defined with Storage Natural Inflow.

Case 9

Hydro cascade system using equivalent formulation:
This example uses a hydro cascade of four storages and four generators as in Figure 5: Cascading Hydro Network.

Figure 5: Cascading Hydro Network


As the water runs downstream in a cascade system, there is also a loss of potential energy during the trajectory. There are different ways it can be handled in PLEXOS which are related to the hydro model selection. In the case of the energy model, properties Generators Efficiency Incr and Waterway Output Scalar Scalar can be used for that purpose as in the following example.

Table 7: Hydro Generator Efficiency
Generator Max Capacity MW Efficiency MW/MW
Adelaide 700 0.68627451
Brisbane 700 0.68627451
Melbourne 220 0.215686275
Perth 100 0.098039216
Thermal 3000 -

First, let's assume we have the following energy data hydro model. In this example, all four storages will try not to run out of water because natural inflows are taken from a deterministic sample. It is also assumed that both upper storages Lake Adelaide and Lake Brisbane have the same amount of natural inflows although they come from independent sources. The rest would take water from the spillways and from the generator releases upstream. Furthermore, spillways don't have delays although they have flowing limits.

Table 8: Waterway Constraints and Output Scalar
Property Max Volume GWh Initial Volume GWh End Effects Method
Lake Adelaide 2900 - Recycle
lake Brisbane 4600 - Recycle
Lake Melbourne 1000 500 Recycle
Lake Perth 500 250 Auto

Note that only Lake Perth is allowed to schedule end volume freely End Effects Method='Auto'.

Table 9: Waterway constraints and output scalar
Property Transversal Time (hrs) Max Flow Min Flow Output Scalar
Spill Brisbane-Perth 0 1000 0 0.098039216
Spill Melbourne-Perth 0 1000 0 0.3125
Spill Perth 0 1000 0

If we take for example 'Lake Adelaide', the result would then show that the end volume for each simulation step must equal the initial value of the next one. Furthermore, the end volume at the end of the simulation (in this case one year) must equal the initial volume as the Generator End Effects Method for storage object 'Lake Adelaide' has been set to 'Recycle'.

Table 10: Results for Case 9. Example of Lake Adelaide Storage Results
Initial Volume
(GWh)		 End Volume
(GWh)		 Natural Inflow
(MW)		 Generator Release
(GWh)		 downstream Release
(GWh)		 Generation
(GWh)
573.71 653.17 287.93 202.09 0 138.69
653.17 878.6 350.57 133.06 0 91.32
878.6 1098.25 371.3 149.4 0 102.53
1098.25 1276.01 371.3 149.4 0 102.53
1276.01 1235.69 322.47 369.65 0 253.68
1235.01 981.16 171.2 421.6 0 289.33
981.16 543.21 14.78 446.91 0 306.7
543.21 63.78 49.4 516.41 0 354.4
63.78 0 309.92 387.41 0 265.87
0 47.41 406.09 354.15 0 243.04
47.41 331.55 456.28 183.86 0 126.18
331.55 573.71 334.82 85.47 0 58.65

Note that the optimal solution did not require any spillage at any time although releasing water from storages is allowed.

Figure 6: Hydro-thermal coordination results for Case9. Energy Model results

Given that this is a deterministic model, the MT scheduler can foresee in advanced the reduction of natural inflows during the months of July and August (dashed line in the figure). The end volumes, for each storage (areas in the figure), drops considerable during the following month. In general, the optimal solution tends to distribute "evenly" the thermal generation avoiding excessive use during the dryer season. However, the risk of optimal deterministic solutions is that minimum end volumes of storages can be binding during water drought stages, leading to aggressive strategy decisions.

Alternative Modelling

Volume Model:
The following example will show how to perform a conversion from the potential energy model to the volume hydro model, leading to same results. For convenience, let's analyse the energy balance at the generator located in the lowest end of the stream chain ('Lake Perth' in Figure 21). Also for convenience, let's assume that the generator efficiencies in pu (e) equals the value of the hydro efficiency (e*) in [MWh/cumec]. If no incomings (inflows) are received, the total output from 'Pert' Generator using the maximum volume of the storage will equal the efficiency of the generator multiplied by the potential energy of the storage.

Figure 7: Equivalent volume model for storage "Lake Perth"

Then, in order to produce the same amount of electrical energy out of 'Pert', the total water flow through the generator must be 10416.6 CMD (see Figure 2). Same applies to other storages upstream.

Table 11: Storage Input for Hydro-Cascade Volume Model
Property Max Volume CMD Initial Volume CMD
Lake Adelaide 120833.3 -
Lake Brisbane 191666.7 -
Lake Melbourne 41666.7 20833.3
Lake Perth 20833.3 10416.7

The total potential energy from each of the two (only) natural incomings will be used by all three generators downstream. Given that the efficiencies sum the unity, as shown in Table Y, the conversion is straightforward:

inflow [MW]=inflow[cumec]

The table presented next, shows the equivalent volume model taking the above assumption.

Table 12: Natural Inflows Used for the Energy and Volume Module
Month Natural Inflows
GWh		 GMD
Jan 1996.98 287.93
Feb 14607.1 350.57
Mar 15470.68 371.3
Apr 15806.24 379.53
May 13436.16 322.47
Jun 7133.39 171.2
Jul 615.77 14.78
Aug 2058.33 49.4
Sep 12913.33 309.92
Oct 16920.51 406.09
Nov 19011.48 456.28
Dec 13950.78 334.82

Note that total volume of the natural inflows is usually reported in CMD (metric system) as follows:

inflow [CMD]=inflow[cumec]*1000*(3600/86400)

As it was expected, the results are equivalent as in the energy model.

Figure 8: Hydro-thermal co ordination results for Case 9. Volume model results.

There are several reasons why the volume (and level) model is more accurate and adequate over the energy model.

  • The Volume and Level models are based on the physical relationships of hydrological objects. Therefore, they are in nature easier to understand.
  • Preparation of cases in the energy model is usually harder because potential energy availability needs to be pre-computed considering every generator downstream.
  • Statistic data and measures are usually given in volume of water.
  • The most important among several drawbacks of the potential energy model is that when there are several ways to which the water can run downstream, there is not an obvious way to determine in advanced the amount of energy that is going to flow through each of the alternative spillways.

7. Hydro Visualization Tools

PLEXOS 6 implements geographical visualization tools for Hydro and Transmission systems. On the main PLEXOS menu, the visualization button will launch the configuration dialog as it is shown in figure

Geospatial data in KML format can be read and displayed in Google Earth. Screenshot of the NZ hydro system in Figure 10: NZ hydro and transmission system in Google Earth visualization.

Figure 9: NZ hydro and transmission system in Google Earth visualization

PLEXOS also supports export of the transmission and hydro systems to Geographic Markup Layout (GML) format which can be read by a number of commercial and freeware viewers such as Cytoscape.

Figure 10: NZ transmission system visualization in Cytoscape