MLF Class

Description:

Marginal loss factor equation

See also MLF Property Reference for a detailed list of properties for this class of object.

This class is specifically designed for the Australian NEM. NEM loss equations include terms for regional demand as well as flow. The simulator (like the NEM market-clearing engine) approximates the loss function with a multi-tranche linear approximation.

You enter the MLF equations directly into the model using special MLF objects, and the simulator will calculate the loss function accounting for all factors including region demand, and from those function generates a linear approximation. This approach has the advantage that loss functions on the interregional interconnectors are calculated every period, ensuring that the simulated losses and interregional prices are as close as possible to an emulation of the market. There is no significant additional overhead or iteration required, so this is a also very efficient approach.

Example:

Class	Name	Category	Description
MLF	LF Murray 330	MLF	Loss factor equation (Murray 330 referred to Thomastown 66)
MLF	LF South Pine 275	MLF	Loss factor equation (South Pine 275 referred to Sydney West 330)
MLF	LF Sydney West 330	MLF	Loss factor equation (Sydney West 330 referred to Murray 330)
MLF	LF Torrens Island 66	MLF	Loss factor equation (Torrens Island 66 referred to Thomastown 66)

Parent Class	Child Class	Collection	Constraint	Child Name
MLF	Region	Regions	LF Murray 330	NSW1
MLF	Region	Regions	LF Murray 330	SA1
MLF	Region	Regions	LF Murray 330	VIC1
MLF	Region	Regions	LF South Pine 275	NSW1
MLF	Region	Regions	LF South Pine 275	QLD1
MLF	Region	Regions	LF Sydney West 330	NSW1
MLF	Region	Regions	LF Sydney West 330	VIC1
MLF	Region	Regions	LF Torrens Island 66	SA1
MLF	Region	Regions	LF Torrens Island 66	VIC1
MLF	Node	Reference Node	LF Murray 330	Murray 330kV
MLF	Node	Reference Node	LF South Pine 275	South Pine 275kV
MLF	Node	Reference Node	LF Sydney West 330	Sydney West 330kV
MLF	Node	Reference Node	LF Torrens Island 66	Torrens Island 66kV
MLF	Line	Line	LF Murray 330	V-SN
MLF	Line	Line	LF South Pine 275	NSW1-QLD1
MLF	Line	Line	LF Sydney West 330	SNOWY1
MLF	Line	Line	LF Torrens Island 66	V-SA

Parent Class	Child Class	Collection	Parent Name	Child Name	Property	Value
System	MLF	MLFs	NEM	LF Murray 330	Intercept	1.0163
System	MLF	MLFs	NEM	LF South Pine 275	Intercept	1.0027
System	MLF	MLFs	NEM	LF Sydney West 330	Intercept	1.0144
System	MLF	MLFs	NEM	LF Torrens Island 66	Intercept	0.9849
MLF	Line	Lines	LF Murray 330	V-SN	Flow Coefficient	0.000095342
MLF	Line	Lines	LF South Pine 275	NSW1-QLD1	Flow Coefficient	0.00023474
MLF	Line	Lines	LF Sydney West 330	SNOWY1	Flow Coefficient	0.000080175
MLF	Line	Lines	LF Torrens Island 66	V-SA	Flow Coefficient	0.00038885
MLF	Region	Regions	LF Murray 330	NSW1	Demand Coefficient	-0.0000028101
MLF	Region	Regions	LF Murray 330	SA1	Demand Coefficient	-0.0000012838
MLF	Region	Regions	LF Murray 330	VIC1	Demand Coefficient	0.000001691
MLF	Region	Regions	LF South Pine 275	NSW1	Demand Coefficient	0.0000017283
MLF	Region	Regions	LF South Pine 275	QLD1	Demand Coefficient	0.0000010083
MLF	Region	Regions	LF Sydney West 330	NSW1	Demand Coefficient	-0.0000059551
MLF	Region	Regions	LF Sydney West 330	VIC1	Demand Coefficient	-0.0000011774
MLF	Region	Regions	LF Torrens Island 66	SA1	Demand Coefficient	-0.0000099266
MLF	Region	Regions	LF Torrens Island 66	VIC1	Demand Coefficient	0.0000022497

Interconnector losses are attributed to the sending and receiving regions in certain proportions. In the Australian NEM, these proportions are fixed constants. Line objects include the property Loss Allocation. By default, this allocation is 0.5, which means losses are attributed evenly to the sending and receiving nodes. The value may be set to any value between zero and one with values above 0.5 meaning that more losses are assigned to the receiving node.

Example:

Line	Property	Value
N-Q-MNSP1	Loss Allocation	0.23
NSW1-QLD1	Loss Allocation	0.5
SNI	Loss Allocation	0.5
SNOWY1	Loss Allocation	.95
V-SA	Loss Allocation	0.6
V-S-MNSP1	Loss Allocation	0.6
V-SN	Loss Allocation	1

Note that losses for the SNOWY1 interconnector are 'normally' allocated in part to Snowy (10%) and NSW (90%), and likewise for V-SN, but for medium term modelling purposes, where no load is attributed to the Snowy region, these allocation factors should be consistent in not allocating any load to Snowy. For short-term modelling, where load are input for Snowy the 'normal' factors should be used (Snowy1 0.95/0.05, V-SN 0.10/0.90).

The NEM uses 10-piece linear loss functions across the entire range of feasible flows, notionally treating maximum import as the 'zero-point' for the approximation. The Transmission setting Max Loss Tranches determines how many loss tranches are used in each direction of flow. Thus, setting this value to 5 will replicate the approach used in the NEM.

The following pictures capture the dynamic MLF and loss approximation over a one-year simulation. There are eight graphs, two for each interconnector. The first chart in the set plots line flow versus loss, treating flows in the 'back' direction as notionally negative. The second chart shows the marginal loss factor (as reported under Marginal Loss Factor). This graph shows clearly the steps in the linear approximation. The green points are the MLF calculated using the 'raw' MLF equations above. The spread of points on each chart shows the amount of variation in the MLF equations due to the dynamic demand elements.

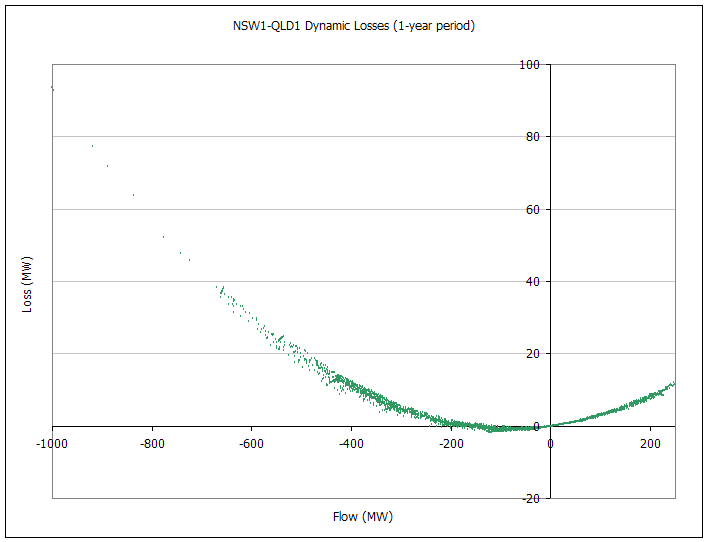Figure 1: NSW-QLD Dynamic Losses (1-year period)

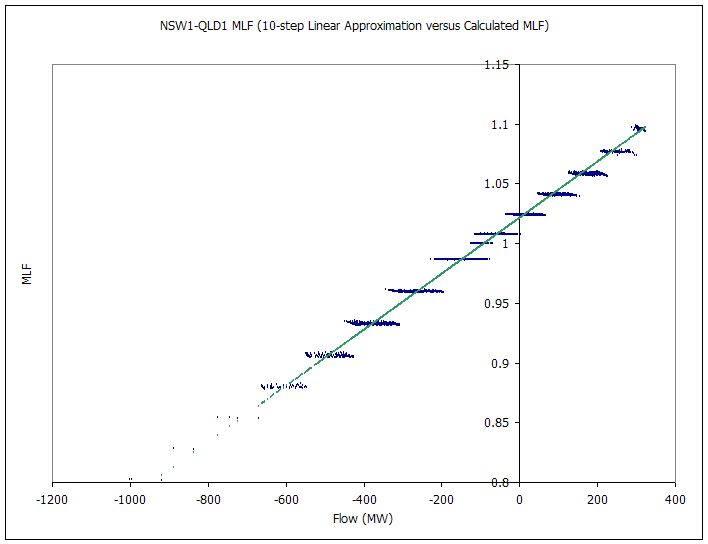Figure 2: NSW-QLD MLF (10-step Linear Approximation versus Calculated MLF)

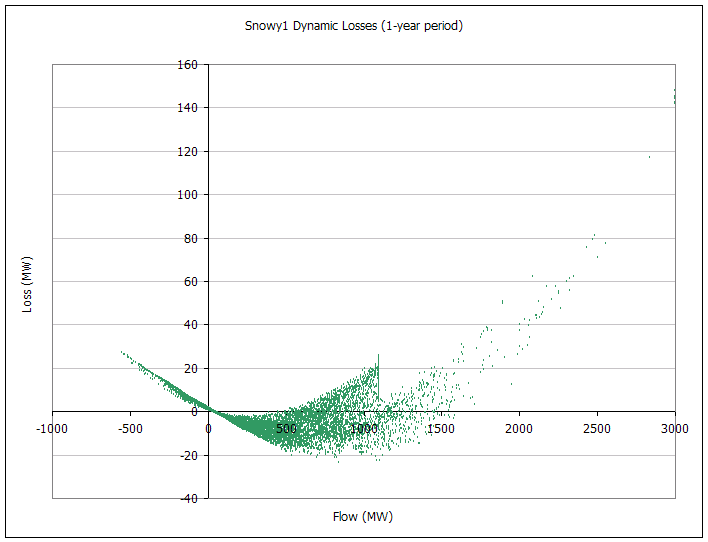Figure 3: Snowy Dynamic Losses (1-year period)

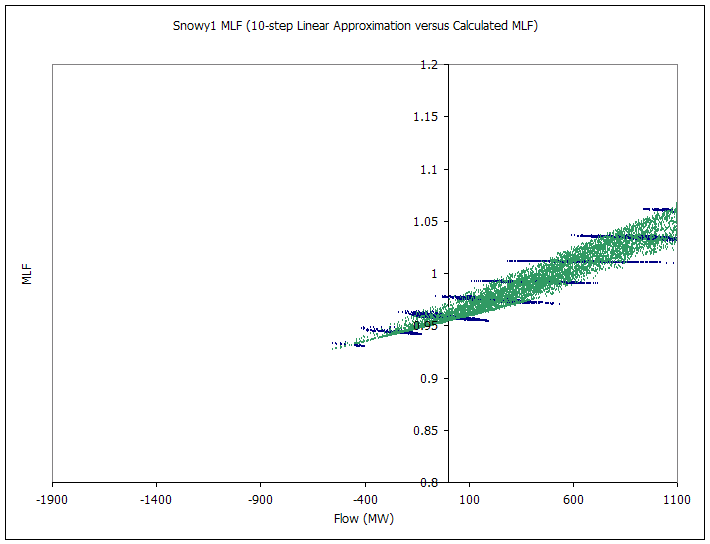Figure 4: Snowy MLF (10-step Linear Approximation versus Calculated MLF)

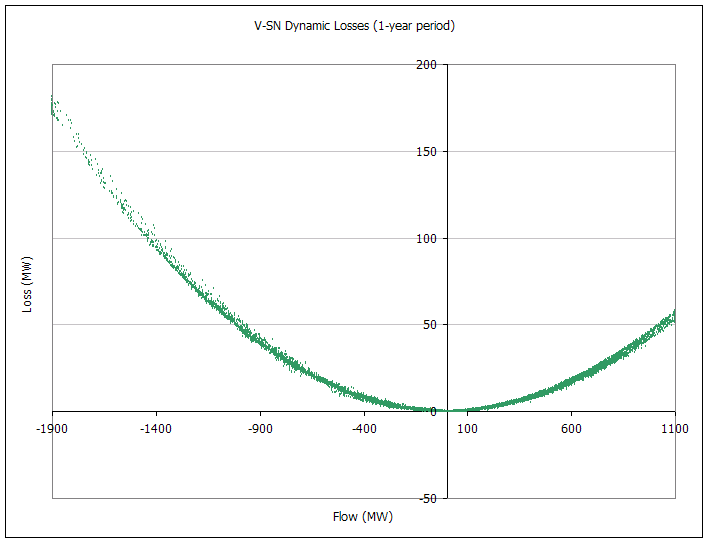Figure 5: V-SN Dynamic Losses (1-year period)

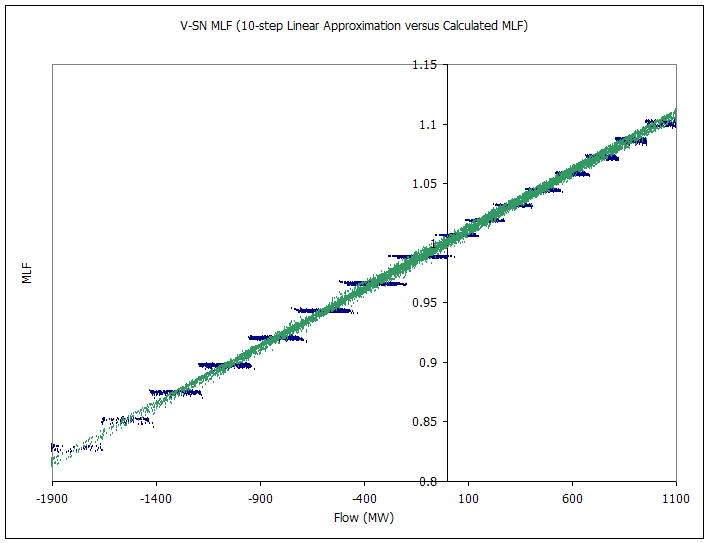Figure 6: V-SN MLF (10-step Linear Approximation versus Calculated MLF)

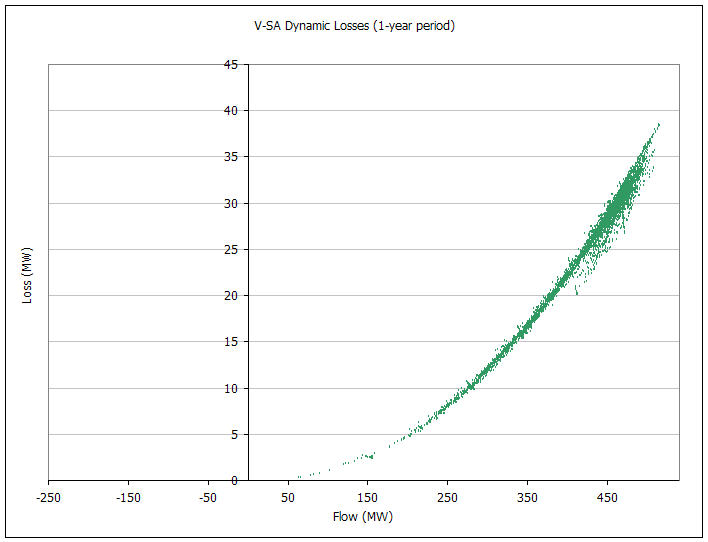Figure 7: V-SA Dynamic Losses (1-year period)

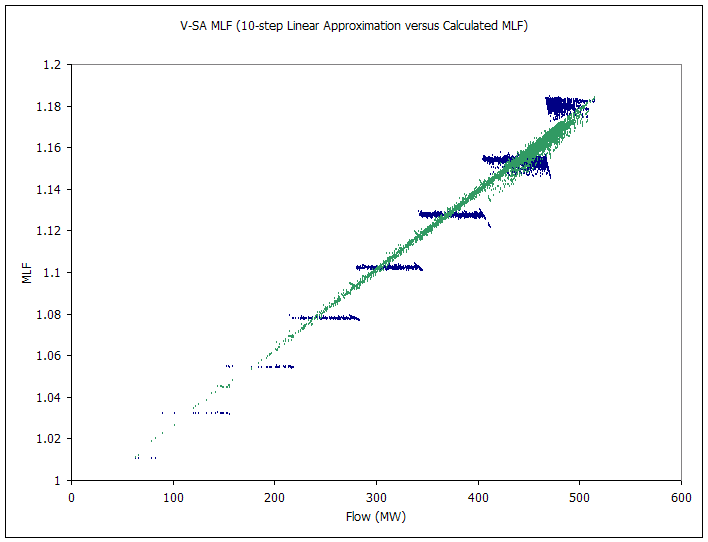Figure 8: V-SA MLF (10-step Linear Approximation versus Calculated MLF)