Hydro-Thermal Co-ordination

Contents

  1. Introduction
  2. Formulation
  3. Example System
  4. Decomposition
  5. Natural Inflows
  6. Energy-constrained Generator

1. Introduction

This section develops an example hydro-thermal coordination model as a way of demonstrating:

2. Formulation

The classic hydro-thermal coordination problem aims to minimise the expected value of thermal generation over some forecast horizon (T) subject to constraints on the availability of hydro generation and storage. The deterministic form of this problem can be expressed as the following optimization problem:

where:
Dt is the electric demand in period t
xt is the thermal generation in period t
ht is the hydro generation in period t
wt is the shortage in period t
st is the storage in period t
nt is the inflow to the storage during period t
\[\bar{x}_{t}\] is the maximum capacity of thermal generation in period t
\[\bar{h}_{t}\] is the maximum capacity of hydro generation in period t
\[\bar{s}\] is the size of the storage
C is the thermal and shortage cost function
V is the value function for storage in the final period T

3. Example System

To illustrate, assume that the thermal supply part of the cost function C is defined as in Figure 1 and that all shortage is priced at the value of lost load (a sufficiently high number) and initially that V = 0 i.e. there is no value of end-of-horizon storage. We simulate a year with demand defined with the daily profile of Figure 2 and monthly scaling factors as in Figure 3. Further, the weekend loads are scaled down by 20%. This gives the annual load duration curve of Figure 4.

For illustration, the hydro is now defined simply as:

The hydro-thermal coordination problem is performed over the horizon T (in this example one year).

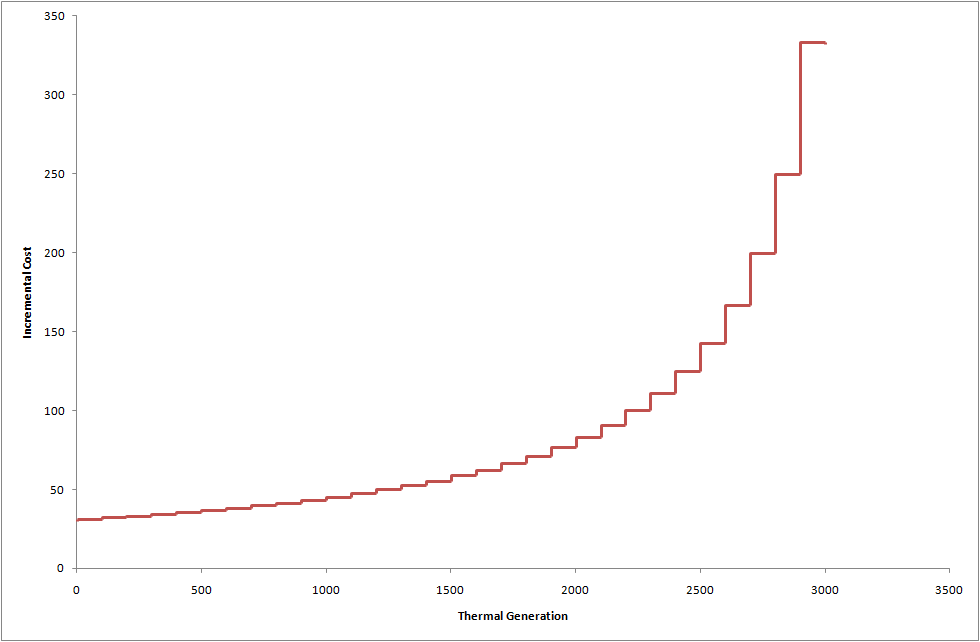Figure 1: Thermal supply function

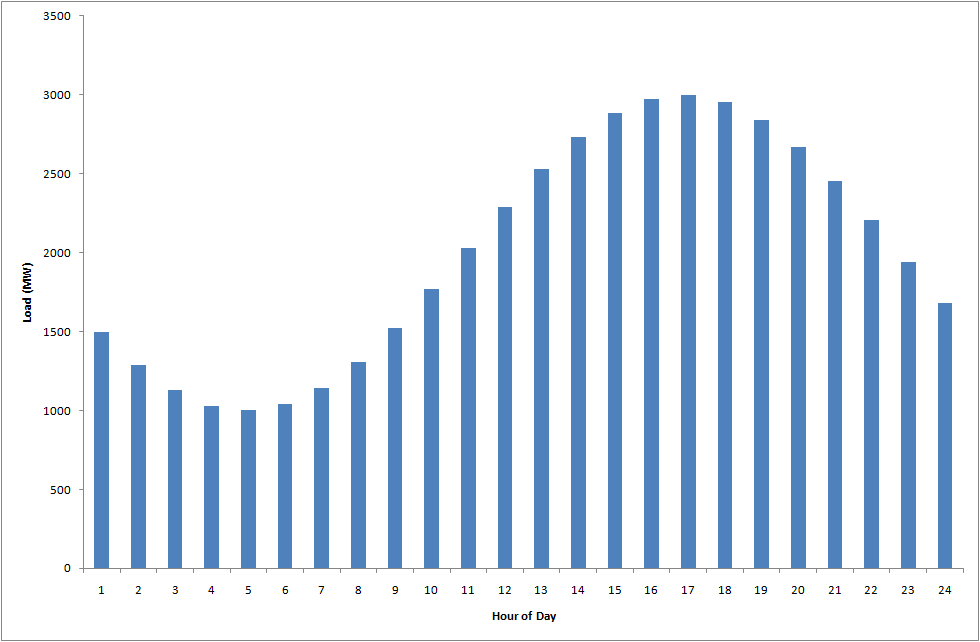 Figure 2: Load by time of day

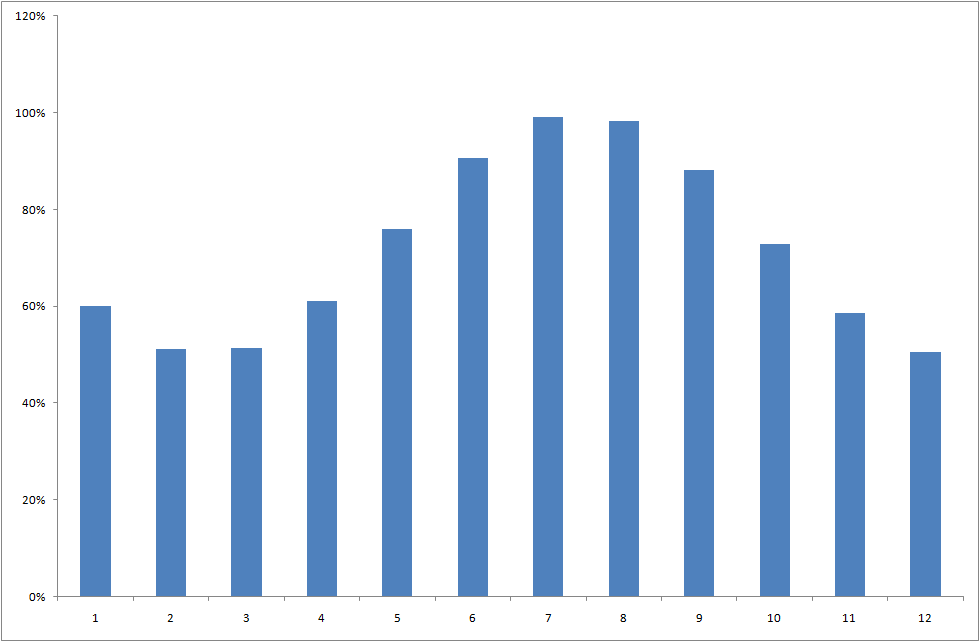 Figure 3: Load scaling factor by month of year

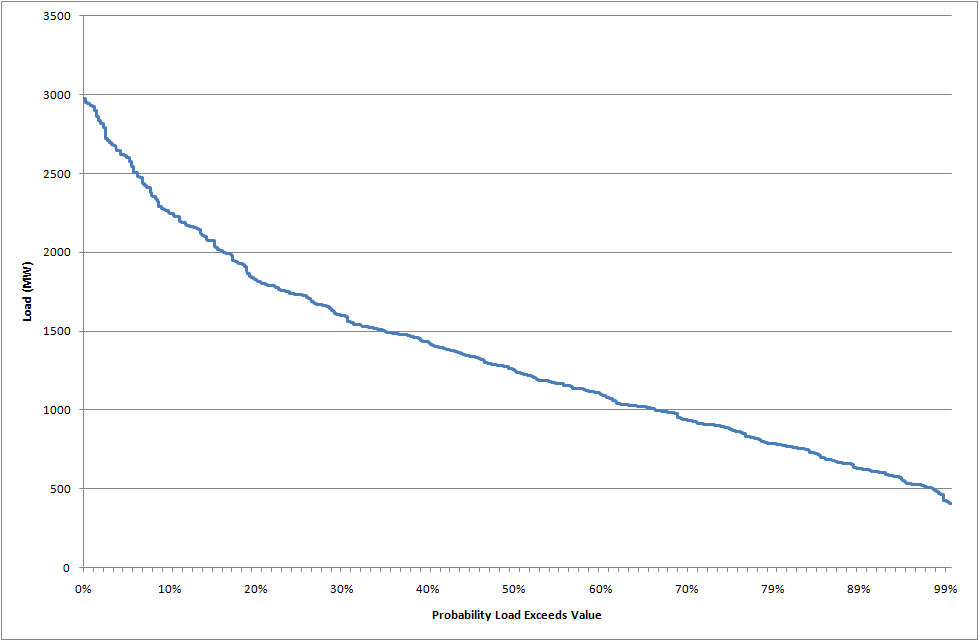 Figure 4: Load duration curve
Case 0

Thermal-only:

As a baseline, if we solve this problem with no hydro utilized, the results in Table 1 are produced. This problem can be solved independently for period t since only the hydro elements form linking constraints between periods.

Table 1: Case 0 results

Month Energy (GWh) Price ($/MWh) Generation (GWh) Thermal Cost ($000)
Jan 841 53 841 33330
Feb 646 47 646 27216
Mar 719 48 719 27216
Apr 830 54 830 33079
May 1056 67 1056 46132
Jun 1234 96 1234 61408
Jul 1397 141 1397 77466
Aug 1365 131 1365 73650
Sep 1199 92 1199 58194
Oct 1020 64 1020 43723
Nov 791 52 791 31030
Dec 712 47 712 26874
Total 11811 82 11811 536517
Case 1

Hydro-thermal solved hour-by-hour:

If we now introduce the hydro, it is clear from the hydro-thermal formulation that the optimal mix of hydro and thermal generation in any given period t is dependent on the solutions in all other periods, since the hydro is limited by the storage volume and the timing of natural inflows.

For example if we 'naively' solve this problem hour-by-hour rather than the whole T periods simultaneously, the optimal solution is to 'use up' the available hydro in each period until the resource is exhausted. The overall results are shown in Table 2, and the storage trajectory (history of end volume each hour of the year) is shown as the blue line in Figure 5 below.

This is the result that is produced when we solve the hydro-thermal coordination problem using only the ST Schedule algorithm with default settings: where the default is in fact to simulate each day independently.

Table 2: Case 1 results

Month Energy (GWh) Price ($/MWh) Generation (GWh) Thermal Cost ($000) Savings (Case 0 - Case 1)
Jan 841 27 841 6383 26947
Feb 646 21 646 3036 21380
Mar 719 22 719 3445 23771
Apr 830 27 830 6589 26490
May 1056 34 1056 12928 33204
Jun 1234 44 1234 20685 40722
Jul 1397 51 1397 27087 50378
Aug 1365 88 1365 47738 25912
Sep 1199 92 1199 58194 0
Oct 1020 64 1020 43723 0
Nov 791 52 791 31030 0
Dec 712 47 712 26874 0
Total 11811 51 11811 287713 248804

4. Decomposition

Clearly the solution shown in Case 1 above is sub-optimal w.r.t. the original formulation. The hydro is exhausted partway through the year, and although there are significant thermal savings over Case 0, there would clearly be more savings overall if some hydro were saved for the later months of the year.

To improve on this solution we must allow the solution method to 'see' the whole simulation horizon and make the correct trade-off between using hydro 'now' versus future periods.

One approach would be to extend the step size of ST Schedule so that the entire horizon is solved in one step of size T. This might work for small problems but is impractical for real sized systems, where the number of equations required would be too large to solve.

Instead we take a two-stage approach, by enabling the MT Schedule (or LT Plan) algorithm in combination with ST Schedule. MT Schedule defaults to simulate in year-long steps, so in this case MT Schedule will find the optimal hydro release policy. By default MT Schedule uses a reduced chronology, rather than simulating every interval, thus if we wish to simulate to full resolution we must also run ST Schedule.

The two (or more) simulation 'phases' are automatically linked together, running MT Schedule first (and/or LT Plan), then ST Schedule but with the ST Schedule hydro release policy guided by solutions of the preceding phase.

In effect long or mid-term phase decomposes the hydro-thermal coordination problem into a number of sub-problems that are then solved by ST Schedule. This multiple-stage approach allows for the efficient solution of very large systems down to full chronological detail.

Case 2

Two-stage optimization with MT Schedule and ST Schedule:

The results for this case are shown in Table 3, and the optimal storage trajectory is the red line.

Table 3: Case 2 results

Month Energy (GWh) Price ($/MWh) Generation (GWh) Thermal Cost ($000) Savings (Case 0 - Case 2)
Jan 841 39 841 16667 16664
Feb 646 38 646 14275 10141
Mar 719 38 719 15833 11382
Apr 830 39 830 16257 16822
May 1056 42 1056 20463 25670
Jun 1234 48 1234 26080 35328
Jul 1397 53 1397 31832 45634
Aug 1365 52 1365 30727 42923
Sep 1199 47 1199 24956 33238
Oct 1020 41 1020 19685 24038
Nov 791 39 791 15960 15070
Dec 712 38 712 15803 11071
Total 11811 44 11811 248537 287980
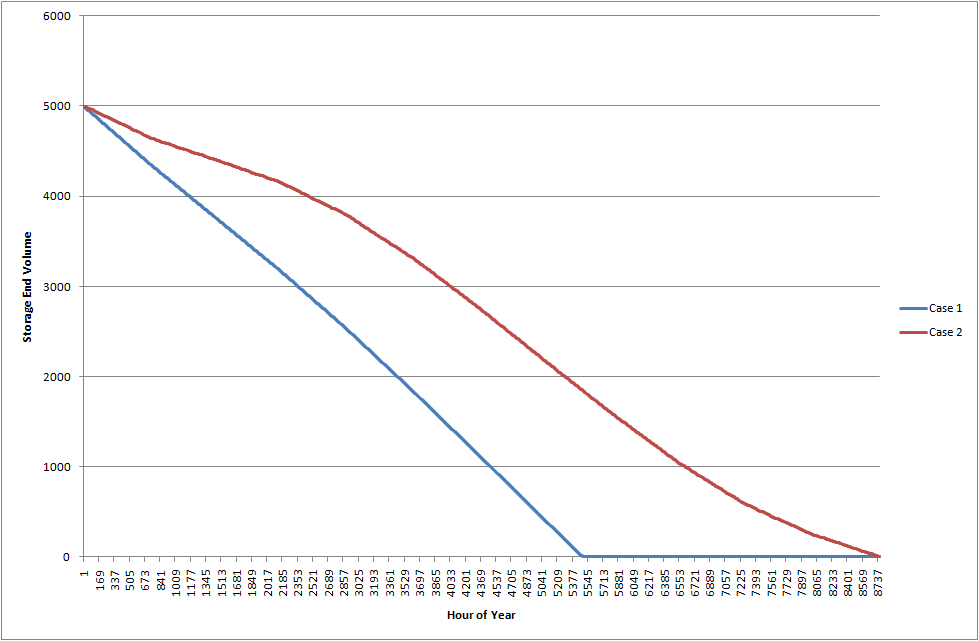Figure 5: Storage trajectories (Cases 1 and 2)

5. Natural Inflows

Thus far we have ignored two elements of the hydro-thermal coordination problem: natural inflows, and the value of end-period storage. To illustrate, assume now that inflows to the storage occur in the monthly pattern shown in Table 4 and illustrated in Figure 6; and that the storage starts the year at 75% full and must return to that level at the end of the year.

These are typical assumptions for modelling storages that 'cycle' over a year or less. In reality some storages have multi-annual cycles, and these can be handled either by decomposing with LT Plan which defaults to multi-annual optimization or by extending the optimization step of MT Schedule.

We define the natural inflow as a dynamic property Storage Natural Inflow. The values are rates, not aggregate quantities, thus we must convert the monthly totals in the "Total (GWh)" column of Table 4 to the equivalent inflow rates in shown in the "Rate (MW)" column.

Defining Storage Natural Inflow automatically invokes the "recycle" method for end storage valuation, meaning that MT Schedule will impose the constraint:

sT=s0

This behaviour can be overridden as shown in see the End Effects Method topic.

Table 4: Natural inflows

Month Proportion Total (GWh) Hours Rate (MW)
Jan 0.04 200 744 268.82
Feb 0.02 100 672 148.81
Mar 0.03 150 744 201.61
Apr 0.05 250 720 347.22
May 0.07 350 744 470.43
Jun 0.08 400 720 555.56
Jul 0.1 500 744 1008.06
Aug 0.15 750 744 1008.06
Sep 0.18 900 720 625
Oct 0.13 650 744 873.66
Nov 0.09 450 720 625
Dec 0.06 300 744 403.23
Total 1 5000 8760 570.78
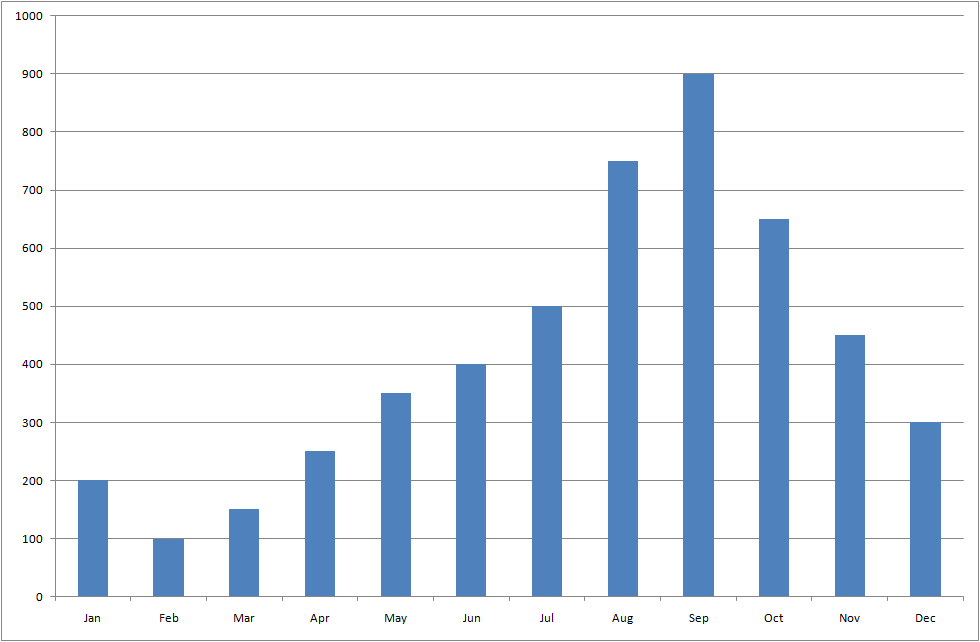Figure 6: Natural inflows by month
Case 3

Natural inflows and recycled storage:

The solution to this case is shown in Table 5. The storage monthly inflows, releases, and end volume is illustrated in Figure 7. Note that the thermal cost in this case is very close to Case 2 indicating that the two-stage optimization has efficiently optimized the use of the storage in order to compensate for the fact that most of the inflows arrive after the peak demand time.

NOTE: This level of optimization might not be achievable in reality because of uncertainty in the flow forecast, and this is discussed in the article, Hydro Reservoirs.

Table 5: Case 3 results

Month Energy Price Generation Thermal Cost Savings (Case 0 - Case 3)
Jan 841 39 841 16843 16487
Feb 646 38 646 14413 10004
Mar 719 38 719 15662 11554
Apr 830 39 830 16172 16907
May 1056 42 1056 20627 25505
Jun 1234 48 1234 26946 35362
Jul 1397 53 1397 31824 45641
Aug 1365 52 1365 30681 42968
Sep 1199 47 1199 24711 33483
Oct 1020 41 1020 19731 23992
Nov 791 39 791 15940 15090
Dec 712 38 712 15917 10975
Total 11811 44 11811 248567 287950
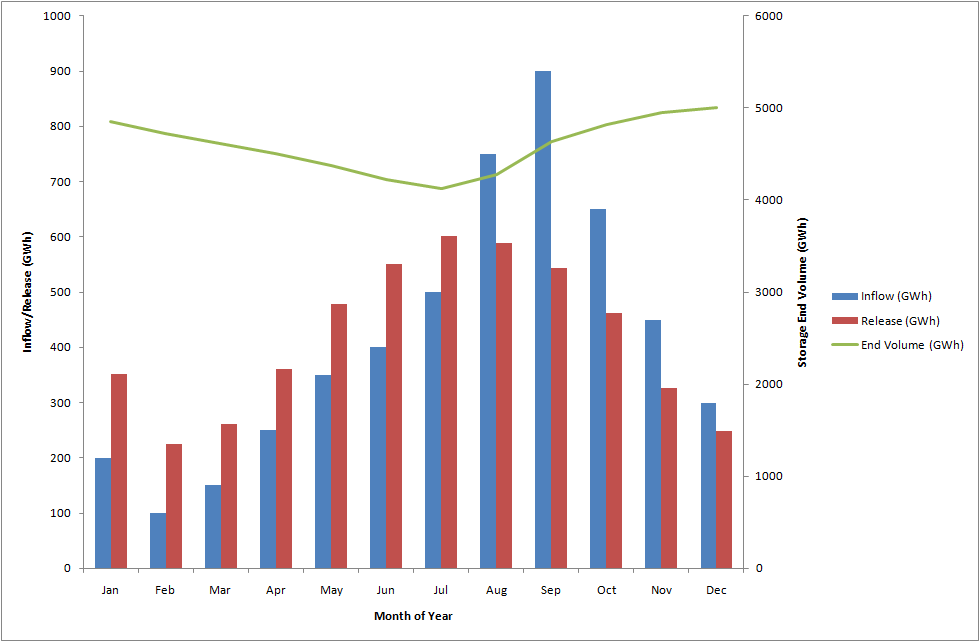Figure 7: Case 3 storage inflow, release and volume by month

6. Energy-constrained Generator

Assuming the hydro systems in our simulation are only as complex as this example or that the available data does not permit the modelling of storages even in this detail we can approximate the hydro system as an energy-constrained generator. This means modelling the hydro using only a Generator object, but adding properties that define:

To illustrate, consider the solution to Case 3 above. This solution can be approximated using a Generator with monthly energy limits and minimum hourly generation as in Table 6.

Table 6: Monthly energy limits and minimum load

Month Energy(GWh) Min Load (MW)
Jan 351.03 0
Feb 277.89 0
Mar 252.94 0
Apr 354.97 0
May 478.96 0
Jun 558.75 134.98
Jul 605.29 191.95
Aug 600.84 199.71
Sep 538.47 81.53
Oct 463.72 0
Nov 326.74 0
Dec 240.4 0
Total 5000

These data are entered as Generator Max Energy Month and Min Load with the Timeslice field set "M1", "M2", ..., "M12". Note how Min Load is a rate, whereas the energy limit is a quantity.

Similar to Case 3 you must enable MT Schedule so that these monthly energy constraints can be decomposed into limits that ST Schedule can follow.

Case 4

Approximation using an energy-constrained generator:

The results for this case are in Table 7. Figure 8 illustrates the generation duration curve for the hydro generator in these two cases: remembering that Case 3 models the hydro with an attached storage and natural inflows, whereas Case 4 models it is a 'simple' energy-constrained generator. These results illustrate how a hydro with storage can be nicely approximated as an energy-constrained generator with energy limits and minimum generation constraints.

In the next section we expand on this example, introducing complexities that cannot be handled using this approximate method and that must be modelled using the more advanced features of the hydro model.

Table 7: Case 4 results

Month Energy Price Generation Thermal Cost Savings (Case 0 - Case 4)
Jan 841 39 841 16887 16443
Feb 646 38 646 14321 10095
Mar 719 38 719 15978 11238
Apr 830 39 830 16361 16718
May 1056 42 1056 20620 25513
Jun 1234 48 1234 25752 35656
Jul 1397 53 1397 31701 45764
Aug 1365 52 1365 30224 43426
Sep 1199 47 1199 24886 33308
Oct 1020 41 1020 10689 24033
Nov 791 39 791 15934 15096
Dec 712 38 712 16190 10684
Total 11811 44 11811 248543 287974
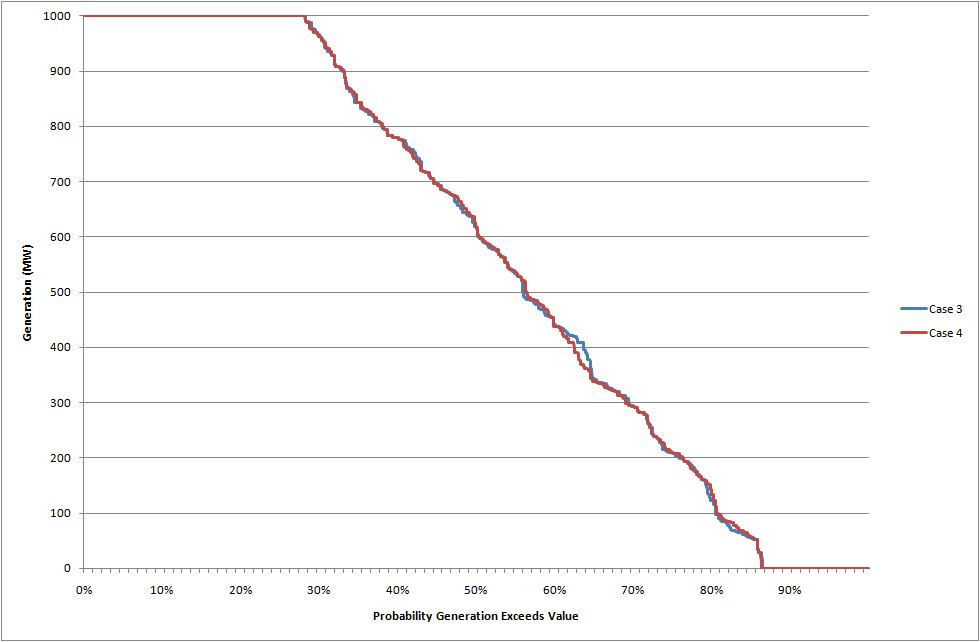Figure 8: Generation duration curves (Cases 3 and 4)