Horizon Look-ahead Indicator
| Units: | Yes/No |
| Default Value: | False (0) |
| Validation Rule: | False (0) or True (-1) |
| Description: | Flag if chronological model used a look-ahead |
Horizon Look-ahead Indicator enables additional look-ahead in ST Schedule.
ST Schedule is a chronological model. It solves a horizon in one or more steps. Each step is a comprised of one or more periods (e.g. hours). You can completely configure the length of these steps and how many are solved using the Horizon properties.
The simulation proceeds by solving these steps in chronological sequence. For example, to simulate a week you might configure ST Schedule to solve seven steps each of one day. Each step is solved as a mixed integer programming problem. The smaller the step size the faster the execution. But with steps of a day each step optimization can look-ahead only one day when optimizing unit commitment (especially with regard to Min Up Time and Min Down Time) as well as hydro and pump storage decisions.
An example is shown below. Here the generator described by the following data faces an uncertain energy price against which to optimize its unit commitment and generation decisions.
Generator Data:
| Generator | Property | Value | Units |
|---|---|---|---|
| 1 | Units | 1 | - |
| 1 | Max Capacity | 10 | MW |
| 1 | Min Stable Level | 4 | MW |
| 1 | Min Up Time | 15 | hrs |
| 1 | Min Down Time | 3 | hrs |
| 1 | Start Cost | 500 | $/start |
| 1 | Fuel Price | 3 | $/GJ |
| 1 | Heat Rate | 7.5 | GJ/MWh |
Simulating two days with ST Schedule configured to solve in two steps of one day each yields the following solution (showing hourly generation, energy price and SRMC):
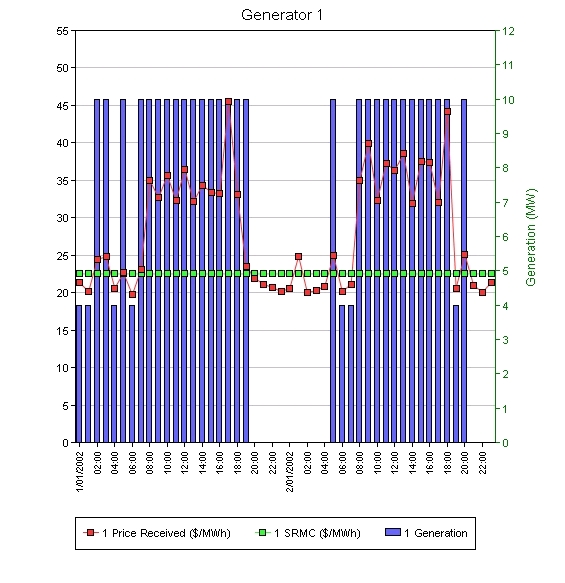 Generator 1
Generator 1
The optimal decision in the first day is to run the unit for the first 20 hours while the price is largely above SRMC. There are a few hours at the start of the day where the energy price is below SRMC but it is optimal leave the unit on given the start cost and minimum down time constraint. The aggregate output for this case is:
| Generator | Property | Value | Units |
|---|---|---|---|
| 1 | Generation | 0.3180 | GWh |
| 1 | Price Received | 31.83 | $/MWh |
| 1 | SRMC | 22.5 | $/MWh |
| 1 | Pool Revenue | 10.1219 | $000 |
| 1 | Generation Cost | 7.155 | $000 |
| 1 | Net Revenue | 2.9669 | $000 |
| 1 | Unit Start Cost | 0.5 | $000 |
| 1 | Net Profit | 2.4669 | $000 |
The chart shows that there is one hour in the second day in which the energy price is above SRMC, and given the high start cost it might have been better to keep the unit on-line at the end of the first day. With the two-step optimization the optimal solution in the second day, given that the unit is off-line at the start of that day, is to start the unit in hour five and generate during the high priced periods of the day, and then shut the unit down again.
Now we reconfigure ST Schedule to allow a look-ahead as follows:
| Property | Value | Units |
|---|---|---|
| Look-ahead Indicator | Yes | - |
| Chrono Look-ahead Type | day | - |
| Look-ahead At a Time | 1 | - |
| Look-ahead Periods per Day | 12 | - |
Now both of the optimization steps will include the day being simulated (all 24 hours) plus an additional 'look-ahead' day modelled as 12 periods (i.e. with each period of that second day being two hours long). The reason we have reduced the resolution of the look-ahead day is to make the simulation as fast as possible.
The resulting optimal solution is as follows:
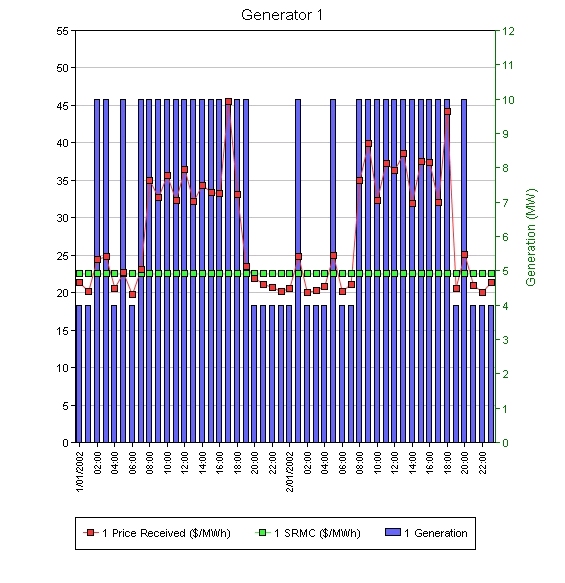 Generator 1
Generator 1
The aggregate generator results are as follows:
| Generator | Property | Value | Units |
|---|---|---|---|
| 1 | Generation | 0.3720 | GWh |
| 1 | Price Received | 30.33 | $/MWh |
| 1 | SRMC | 22.5 | $/MWh |
| 1 | Pool Revenue | 11.2825 | $000 |
| 1 | Generation Cost | 8.37 | $000 |
| 1 | Net Revenue | 2.9125 | $000 |
| 1 | Unit Start Cost | 0.0 | $000 |
| 1 | Net Profit | 2.9125 | $000 |
The optimization was able to look-ahead and know that it is better to keep the unit on-line overnight and save the cost of a unit start up the next day, as well as capture the high price early in the second day. The overall profit of the plant has increased from 2466.90 to 2912.50, an improvement of 445.6.
In practice you should use ST Schedule look-ahead in cases where unit commitment decisions must be precisely optimized. The amount of look-ahead (including the step) should be sufficient to recover start costs and/or evaluate the longest up or down time constraint.
Note that the amount of look-ahead must be added to the planning horizon. For example in the above case the planning horizon must be three days long so that both ST Schedule steps can have the defined look-ahead.