Nodal Contingency Islanding
Contingency outages that create islands cause power imbalances in each island. If x MW of power was being imported into an island before the contingency, then post-contingency the generation within the island would need to increase by x MW to make up for the loss from imports. Similarly, if x MW was exported from an island in a pre-contingency scenario, then post-contingency the generation would need to decrease by x MW.
Theoretically speaking, it is possible to accurately determine the post-contingent dispatch (and therefore post-contingent flows) by re-writing the power flow equation for all islands. However, this presents a practical problem. In addition to the set of power flow equations for the base N-0 system, each islanding contingency being modeled would need to have its own power flow equations for every island. Even for small systems, the theoretically accurate approach would result in the problem size growing beyond the computational and memory limitations of standard computers. Furthermore, given Aurora's primary role as a production cost model, any gain in accuracy from a theoretically accurate approach is likely to have little impact.
The Contingency Islanding logic approximates the theoretical solution while avoiding the computational limitations.
The logic is best illustrated via an example setup for an islanding contingency.
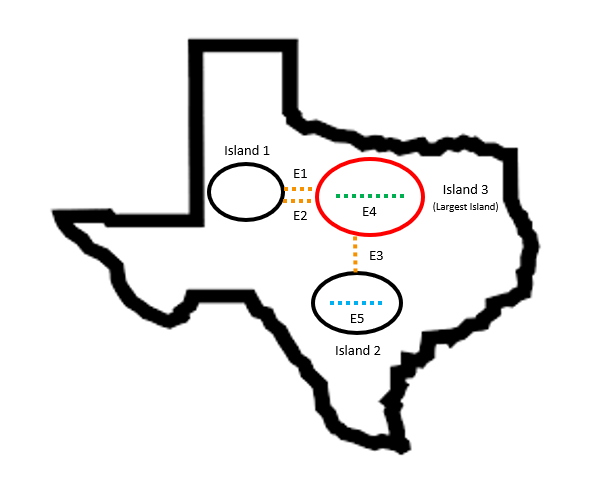
Lines E1, E2, and E3 form the islanding cutset, line E4 is entirely within the largest island, and line E5 is entirely outside the largest island..
Determining Post-Contingent Flow
Consider the N-5 contingency illustrated in the figure above. Outages of the five specified contingent elements creates three islands, represented as circles in the illustration. The largest island, i.e., the island with the largest number of buses, is highlighted in red.
Each of the five contingent elements can be classified into the following three groups:
-
Islanding Cutset: This is the set of elements that connects two different islands; outages on this set of lines is what causes the islands. These elements are highlighted in orange.
-
Within Largest Island: This is the set of elements that are fully within the largest island. Outage of this set of lines doesn't change the island structure. These elements are highlighted in green in the illustration.
-
Outside Largest Island: This is the set of elements that are fully outside the largest island. Outage of this set of lines doesn't change the island structure. These elements are highlighted in blue in the illustration.
To determine the post-contingent dispatch in the largest island for the N-5, Aurora does the following steps:
-
Categorize each of the 5 elements into the three categories described above. As shown in the illustration, lines E1, E2, and E3 form the Islanding Cut-Set, line E4 is entirely within the largest island, and line E5 is entirely outside the largest island.
-
Determine pre-contingent net Imports/Exports over the islanding cut-set. Let us represent this as f.
-
For each generator g in the largest island determine the approximate post-contingent dispatch as:
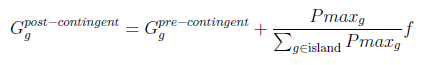
where Gg represents the generation by generator g, and Pmaxg represents the Pmax value specified for the generator in the Network Case Input file (.alfc).
The crux of the approximation is that all generators in the largest island respond to the loss of net import (or export) over the islanding cutset. Furthermore, generator response is proportional to its Pmax.
-
Once the approximate post-contingent dispatch is determined, flows are calculated on all branches within the largest island, including the elements that were categorized as "Within Largest Island" in step 1, e.g., line E4.
-
The final post-contingent flows for the set of monitored elements are determined by adjusting the flows for outage of "Within Largest Island" contingent elements.
Once the post-contingent flows have been calculated for the monitored elements, Aurora checks for violations of the contingency flow limits. If any violations are found, appropriate constraints are added.
Additional Resources
Modeling Details
Nodal Contingency Islanding
