CCGT
Click here to see this page in full context

Combined Cycle

Contents

  1. Introduction
  2. Waste Heat Transfer and Efficiency
  3. Unit Commitment and Outages
  4. Duct Burner
  5. The Example Solved
  6. Ancillary Services
  7. Heat Load and District Heating
  8. Modelling CCGT Using Heat Node
  9. Modelling CCGT Configuration
    1. Decision Variables:
    2. Generic Constraints:
    3. Special Technical Constraints:

1. Introduction

PLEXOS models combined-cycle plant by explicitly tying the waste heat output of one or more units to the heat input of another unit. Specific features available in this model include:

  1. Waste heat from units of different size and efficiency.
  2. Accounting for boiler efficiency.
  3. Steam- turbine heat rate as a function of loading level.
  4. Duct- burner model.
  5. Exogenous steam loads e.g. for loads associated with co-generation plant.

The PLEXOS combined-cycle model is shown in Figure 1. In this representation:

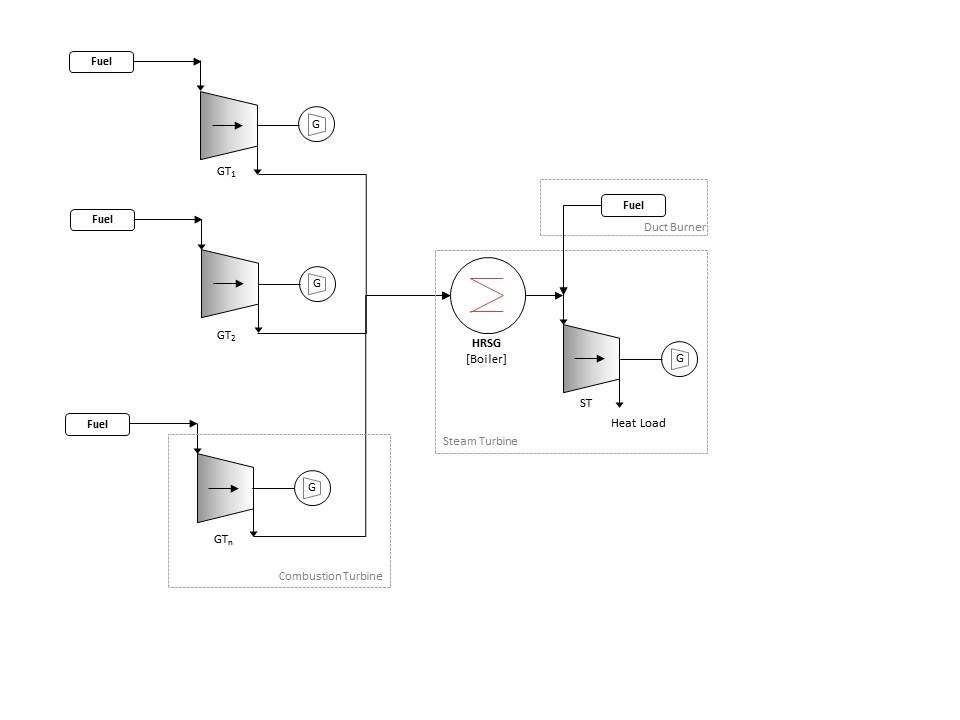Figure 1: Combined Cycle Model


this article follows and example based on a 2 x 1 setup with the following characteristics:

Table 1 presents the CT unit data for this case, Table 2 the ST data. For the example, assume there are two identical CT units (CT1 and CT2).

Property Value Units Band
Units 1 - 1
Max Capacity 160 MW 1
Min Stable Level 160 MW 1
Heat Rate Base 200 MMBTU 1
Heat Rate Incr 8000 BTU/kWh 1
Heat Rate Incr 8800 BTU/kWh 2
Heat Rate Incr 9600 BTU/kWh 3
Heat Rate Incr 9800 BTU/kWh 4
Heat Rate Incr BTU/kWh BTU/kWh 5
Load Point 64 KW 1
Load Point 88 MW 2
Load Point 112 MW 3
Load Point 136 MW 4
Load Point 160 MW 5
Min Up Time 4 hrs 1
Min Down Time 2 hrs 1
Table 1: CT Unit Data
Property Value Units Band
Units 1 - 1
Max Capacity 190 MW 1
Min Stable Level 0 MW 1
Boiler Efficiency 80 % 1
Heat Rate 12700 BTU/kWh 1
Table 2: ST Unit Data


Note carefully that the ST total capacity is the sum of the 'normal' capacity plus duct burner capacity - we will discuss how to limit the duct burner contribution below.

Assume that a fuel called GAS has been defined. Given this, the relevant memberships for the combined-cycle plant are shown in Table 3. All three generating units use GAS (Point 1 in ). Note that the ST need not have a fuel membership because it receives waste heat from the CTs via the boiler, but this is included to model the duct-burner facility (Point 2 in ) i.e. the fuel burned by the ST will represent the duct burner use, with efficiency adjusted according to the boiler efficiency.

Collection Parent Name Child Name
Generator Fuels CT1 GAS
Generator Fuels CT1 GAS
Generator Fuels ST GAS
Generator Heat Input ST CT1
Generator Heat Input ST CT2
Table 3: Memberships for CC Plant


For clarity, this example is deliberately simplified, so it is important to note that you have access to all the usual generator modelling features for each of the CT and ST units and there are no preset limits on the configuration (2 × 1, 3 × 1, 4 × 1, etc).

2. Waste Heat Transfer and Efficiency

Waste heat is 'transferred' from one generator to the next using the Generator Heat Input collection. In our example the ST unit takes waste heat from both CT1 and CT2 as defined by the memberships in Table 3.

The amount of heat transferred from the CTs to the boiler is equal to the fuel input to the CTs less the electric output of the CTs (at notional maximum efficiency). Note that you should choose the appropriate metric or imperial units model (under Settings in PLEXOS) so that the efficiency conversion is computed consistent with the input heat model e.g. Using 100% efficiency equals 3.6 fuel units per megawatt hour in metric or 3.412 in imperial.

The waste heat is then passed through the boiler before being used in the ST. The boiler is modelled as part of the ST and its efficiency is defined using the Boiler Efficiency property e.g. 80%. By default this efficiency is 100%.

The ST unit will produce electric output from the steam output of the boiler according to its heat rate i.e. the steam input acts just like a 'free' fuel source. The waste heat produced by ST is the remaining energy after generation, which is defined differently from the input waste heat. (See Waste Heat)

Additional fuel can be injected to the boiler (duct burner facility) as described below.

3. Unit Commitment and Outages

The ST unit cannot operate unless at least one of the CT units is operating. PLEXOS automatically enforces this rule when the Generator Heat Input membership is defined between the units.

Generator outages may be modelled on CT and ST units in the usual manner - as described in [2]. Because PLEXOS explicitly models heat transfer the overall efficiency of the combined-cycle plant will correctly account for the number of CTs on-line and the heat rate as a function of the CT and ST units.

When all CT units are out of service the ST will not operate, however the CT units may operate independently of the ST - but would only do so if the price they receive is high enough to at least compensate them at their raw CT heat rate.

4. Duct Burner

Some combined-cycle plant can boost generation from the ST part by injecting fuel into the ST. This duct burner facility is modelled in PLEXOS by adding a fuel membership to the ST unit, as in Table 3.

By default the duct burner capacity would be limited only by the ST capacity so we use the property Generator Fuels Max Input to set a limit on the fuel injected into the duct burner, as in Table 4. The figure of 625 is the ST heat rate multiplied by the 50 MW capacity of the duct burner.

Note that the fuel injected at the duct burner enters AFTER the boiler and thus is NOT subject to the efficiency of the boiler component.

Membership Property Value Units
Generator (ST) Fuels (GAS) Max Input 625 MMBTU
Table 4: Additional Properties for Duct Burner Operation

5. The Example Solved

Need to provide example database for this case.

Now assume that the combined-cycle plant generates into an external energy market with an uncertain forward price. The illustrations below present a selection of the results from a sample week.

Referring to Figure 2 it is clear that the automatic logic constraints that PLEXOS produces that control when the steam turbine can operate are in force; also the steam turbine output varies according to how much waste heat is coming from the CT units, and this is a function of their loading level and heat rate. The noticeable spike in ST output during high priced periods Figure 3) is produced by the duct burner capability and this is easily seen from the fuel offtake results (Figure 4) in which the ST unit only uses fuel when it is utilizing the duct burner facility.

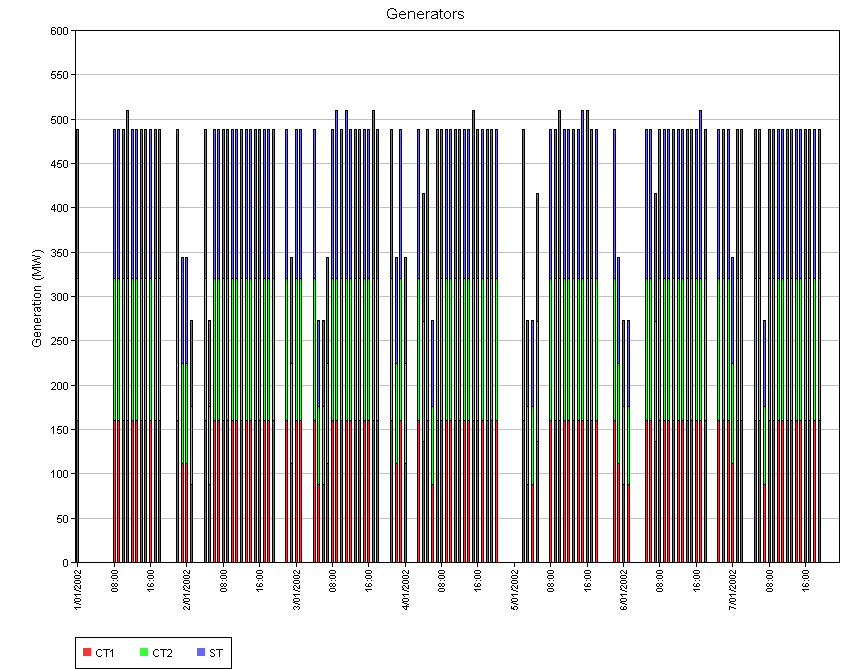Figure 2: CCGT Generation by Unit

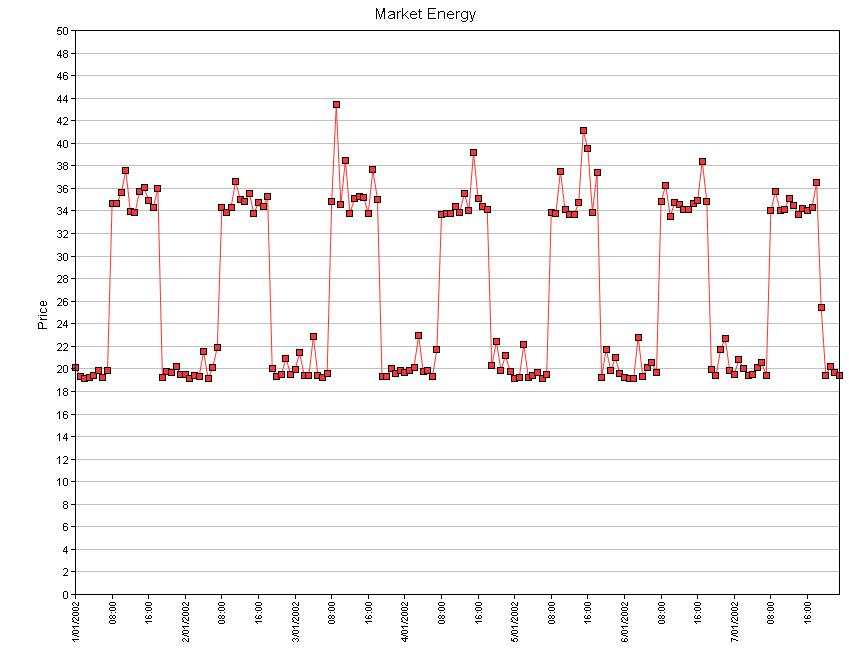 Figure 3: Energy Market Prices (endogenous stochastic variable)

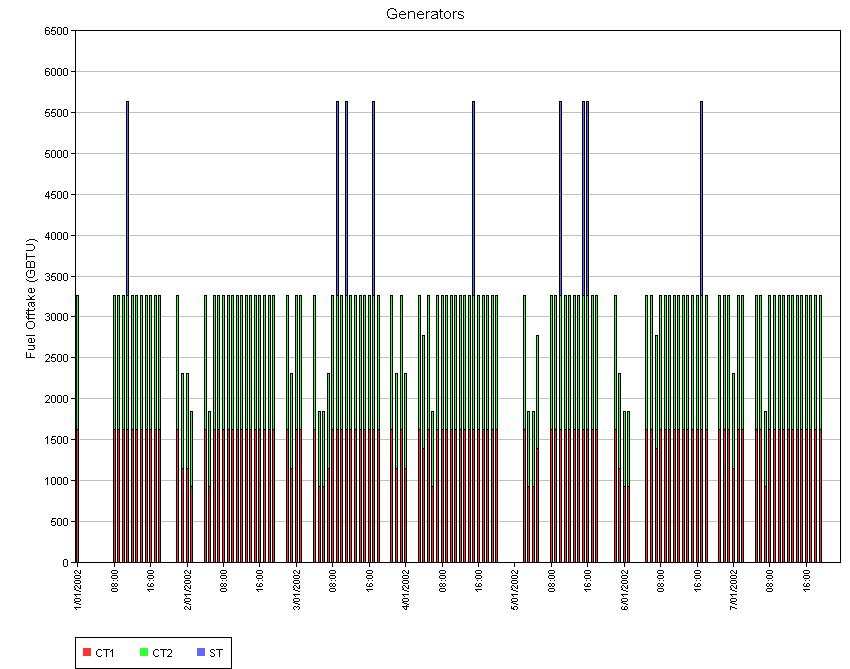 Illustration 3: CCGT Fuel Use by Unit

6. Ancillary Services

Both CT and ST units may provide reserve-as described here.

7. Heat Load and District Heating

An exogenous heat load can be placed on the ST unit using the property Heat Load described in [4], and this is useful for modelling co-generation plant. This load will always be met if physically feasible.

PLEXOS can also arbitrage optimally between electric production and supply of heat to an external heat market (which might represent a contract to supply district heating for example)-these options are described in Market class.

8. Modelling CCGT Using Heat Node

Another alternative way to model the CCGT from PLEXOS 7.6 version is using the new heat class feature. GT generators are connected to a heat node via Heat Output Nodes membership. ST generators are linked to the same heat node via Heat Input Nodes membership. The auxiliary boiler can be modelled by the Heat Plant class. See Heat Modelling for more details.

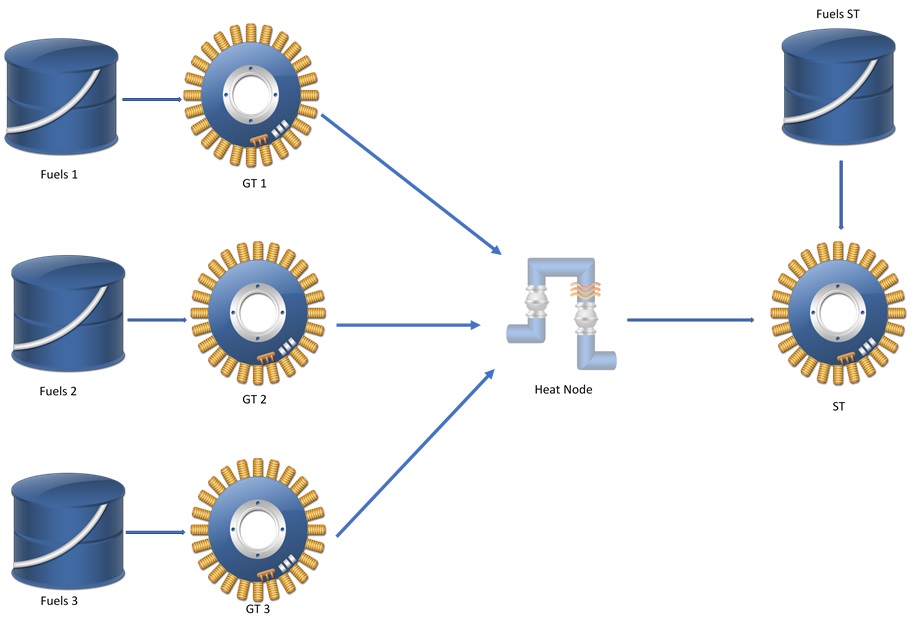Figure 4: Model CCGT using heat class.

Modelling CCGT Configuration

When there are 2 or more GT generators connecting to a same ST generator (or even more ST), there exists several CCGT configurations or combinations. For example, 1 GT runs with the ST or 2 GTs runs parallel with ST. Currently, PLEXOS does not model the configuration specifically. However, it can be achieved using the Generic constraints and Decision Variables. This section presents an example on how to model the CCGT configuration for 3 GT and 1 ST. Please contact Energy Exemplar staff for a copy of the example model.

In this example, we model 3 GT and one ST. There are 3 possible configurations for this CCGT operation.

9.1 Decision Variables:

Creating 3 decision variables (called GT1alone, GT1+GT2, GT1+G2+GT3). They are all binary decision variables (Type = Integer, Lower bound = 0, Upper Bound = 1).

9.2 Generic Constraints:

  1. Configuration GT1 Alone:

GT1Alone =⁢ [UnitGeneratingCoefficient]_GT1
G1Alone + [UnitGeneratingCoefficient]_GT2 =< 1
G1Alone + [UnitGeneratingCoefficient]_GT3 =< 1

  1. Configuration GT1&GT2&GT3

GT1&GT2&GT3 =< (UnitGeneratingCoefficient]_GT1 + UnitGeneratingCoefficient]_GT2+ UnitGeneratingCoefficient]_GT3)/3
GT1&GT2&GT3 =< (UnitGeneratingCoefficient]_GT1 + UnitGeneratingCoefficient]_GT2+ UnitGeneratingCoefficient]_GT3) - 2.99

  1. Only one configuration state is allowed.

GT1Alone + GT1Alone + (GT1&GT2) + (GT1&GT2&GT3) =< 1
With the above constraints and decision variables, we can know which configuration is active.

9.3 Special Technical Constraints

If there is any special CCGT configuration rule required, additional constraints can be added using the above decision variables.

For example, we can't move from state GT1&GT2&GT3 to GT1alone and vice versa. In this case, we need to write this constraint (using time lag)

GT1Alone(t-1) + GT1&GT2&GT3(t) =<1

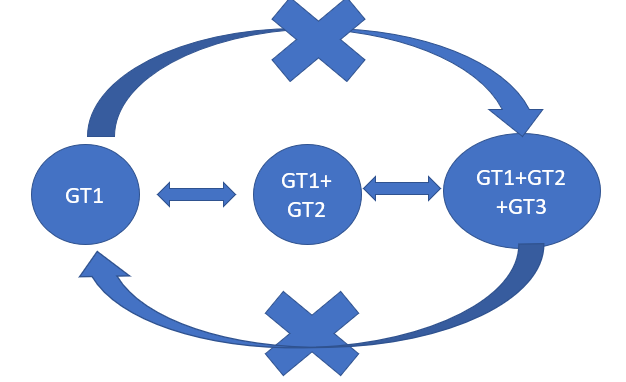Figure 5:Configuration Rule.

Another common requirement is modelling the transition time from one configuration to another. For example, the transition from state GT1Alone to GT1&GT2 is 45 minute. First of all, we need to know the number of intervals covering the transition time. N = [Transition Time]/[Interval length]. Says the simulation interval is 15 minute, we have N = 45/15 = 3 Using the time lag feature, we will write N generic constraints as:

GT1Alone(t) + GT1&GT2(t) =< 1 (1)
GT1Alone(t) + GT1&GT2(t+1) =<1 (2)
...
GT1Alone(t)+ GT1&GT2(t+N) =<1 (N)
This means that if GT1Alone is active, the next 3 intervals (45 minutes), state GT1&GT2 cannot be used.

References