Reserve Class

Description:

Ancillary service

See also Reserve Property Reference for a detailed list of properties for this class of object.

The Reserve class of objects in PLEXOS defines ancillary services for cooptimization with the energy dispatch.

Background

There are a number of constraints imposed on the dispatch by the physical operating limits of the generating units and the transmission network. Among these constraints is the requirement that the system operates within an acceptable range of voltages, frequencies, and power flows even if a major generator or transmission link fails.

For example, in the New Zealand and Singapore power systems, it is the under-frequency constraints that are the most limiting, particularly following a failure of large generating unit or transmission link. In New Zealand these constraints are so severe that, on occasion, there has been more capacity committed to reserve provision than to generation in the receiving region. In the Australian NEM however, both under and over frequency events can be significant, so both 'raise' and 'lower' capabilities must be maintained.

In defining instantaneous reserve in the under-frequency context, the single contingency situation is defined, in which there is a failure of the largest unit generating, the largest battery discharging, or a major transmission line. Immediately following the disruption the system frequency will fall from the nominal value and reach some minimum before the combination of voluntary load interruption and increased generator load addresses the generation-load imbalance. To meet the imbalance between the reduced generation and the load, several events may occur in combination:

• Governors in the automatic generation control systems that react to the falling system frequency increase output from generators that are already operating - this is known as partially loaded spinning reserves (or simply "spinning reserve");
• Generators operating as synchronous condensers i.e. synchronized to system frequency but carrying no load, e.g. hydro units operating in tail-water depressed (TWD) mode, are brought up to generate; and
• Batteries may respond to the falling system frequency by changing their active power set point (i.e. charging less and/or discharging more);
• The load taken by selected customers (or by pumped storage generators) may be reduced - this facility, called interruptible load is only available where suitable contracts, and automatic signalling mechanisms have been put in place.

Interruptible load reserve is straight-forward to model in a market-clearing model because it simply subtracts from the reserve requirement subject to its incremental cost. Generator reserve capability is necessarily co-joined with generator dispatch, and must be handled in a more sophisticated manner. The following sections describe generator reserve capability in general and develop the energy and reserve cooptimization first described by Drayton [1], and included in the New Zealand, Australia, and Singapore electricity markets. This approach forms the basis for the cooptimization approach in PLEXOS and is widely applicable to ancillary services modelling for international markets.

Ancillary Services

Several classes of ancillary services are required:

• regulation (frequency keeping) capability;
• fast response reserve (for various time frames such as 6-60 seconds, or several minutes);
• non-spinning (or replacement) reserves; and
• inertia.

In addition, both regulation and fast response reserve can be defined as either 'raise' or 'lower' requirements. The lower requirement is needed in case of a sudden drop in load e.g. a major industrial load trips, or a transmission line goes out of service suddenly leaving the exporting region with surplus generation.

The simulator provides a broad and comprehensive capability for calculating economic dispatch constrained by all these ancillary services (reserve) constraints. This is achieved by integrating reserve constraints into the mathematical framework for dispatch and pricing to create a cooptimization of energy and reserves.

The Reserve class is generic enough that it can be used to model any class of ancillary service where provision is made by:

• setting aside spare capacity on running generators, or
• interruptible load reserves including interruptible pumping load, or
• synchronous condenser plant, or
• plant on stand-by (non-spinning)

Reserve Requirement

Ancillary services requirements imply that the choice of generating units, and their level of generation depends not only on unit availability and cost, but also on the impact each unit can have on system frequency during the critical period immediately following a contingency. Some plant provides a rapid initial response but then 'runs out of steam'; other plant can only provide delayed response, while yet other plant provides a steady increase in output.

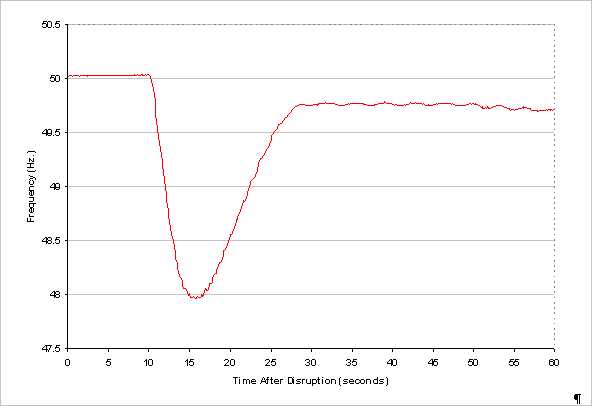
The following illustration is a trace of the system frequency following the loss of a 250 MW generating unit in the New Zealand system. The frequency will generally reach a minimum within five to seven seconds. It is important that the frequency remains above 48 Hz (from its nominal value of 50 Hz), a requirement referred to as the 'minimum frequency constraint'. In addition, there must be sufficient surplus generation capacity available to return the system close to 50 Hz within 60 seconds of the contingency, a requirement referred to as the 'surplus reserve constraint'.

In the New Zealand spinning reserve market, these are referred to as the fast and sustained, or 6 and 60-second reserve constraints.

The Australian NEM includes both 6, and 60 second reserve as well as 5-minute reserve. It also includes both raise and lower services for under and over frequency events respectively.

The Type attribute selects the type of service (spinning, non-spinning, raise, lower, etc),

The term 'raise' refers to a service for generators' capability to raise output in response to an under frequency event, likewise 'lower' refers to a service where generators decrease (or unload) in response to an over-frequency event.

Ancillary services (Reserve objects) can be switched on/off using the Is Enabled property. This property supports scenario tags.

The Min Provision sets the minimum requirement for the service.

The reserve requirement can also be set dynamically based on the highest generation level of the set of Generators defined in the Generator Contingencies set and the set of Batteries defined in the Battery Contingencies set.

Further, the reserve requirement can be based on a percentage of load using the Load Risk property.

The 'final' requirement is the maximum of:

• Min Provision;
• the largest unit generation in the Generator Contingencies set;
• the largest battery generation in the Battery Contingencies set;
• the largest line flow within the Line Contingencies set; and
• the largest of the Load Risks.

You can add a 'static' requirement to the resulting requirement with the property Static Risk.

If the reserve requirement exceeds the capability of all reserve sources then a shortage will be recorded, priced at the value of reserve shortfall ( VoRs). Note that infeasibilities may result if VoRs is not set and the reserve requirement is impossible to meet. Thus it is good practice to define VoRs.

Generator Reserve Providers

The generators that can provide reserve are added to the Generators collection of the Reserve object. Various properties on this collection can be set to control the amount of and cost of reserve available:

• Max Response;
• Max Pump Response for pumped storage interruptible load reserves;

as well as:

• Min Provision;
• Min Spinning Provision for spinning reserves;
• Min Regulation Provision for generators defining a Regulation Range;

By default all generators in the Reserve Generators collection can provide the reserve. Alternatively the choice of generators providing the reserve (out of this set) can be optimized as a 'choice' variable in the mathematical programming problem. In this case the minimum and maximum limits on provision are applied if-and-only-if the generators are selected to provide reserve. See the Unit Commitment topic.

Battery Reserve Providers

Batteries which can provide reserve are added to the Batteries collection of the Reserve object. As for generators, properties on this collection can control the quantity and cost of reserve available.

• Max Response;
• Min Provision;
• Min Spinning Provision; and
• Min Regulation Provision.

Spare Capacity Reserves

In the following we discuss the approach taken to modelling spare capacity reserve of the 'raise' type in particular.

The reserve providing potential of a generating unit (or multi-unit station) depends on the amount of generation and hence the amount of spare generation capacity. Reserve capability increases as more energy is produced but is ultimately limited by spare capacity, which falls as the unit approaches full loading. Ignoring factors such as minimum loading levels and efficiency effects, a continuous approximation to a unit's set of feasible operating points for instantaneous reserve can be plotted in the space of all combinations of output and generation capacity, as illustrated here:

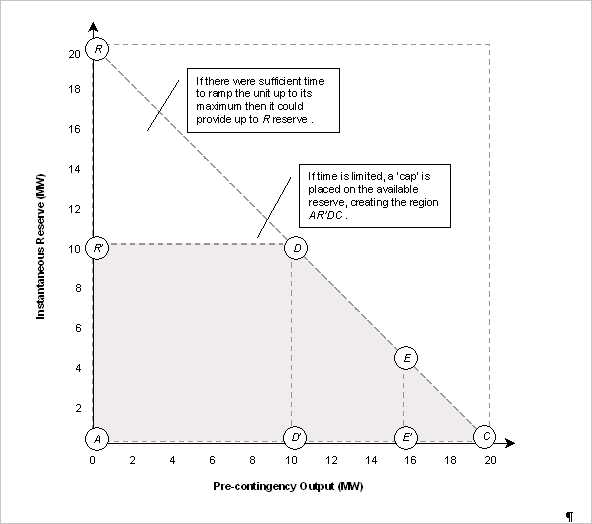
The x-axis represents the units energy output prior to the contingency and the y-axis represents the reserve it could provide following a contingency. Point A represents zero output and reserve, while C represents maximum energy output with zero reserves. Energy plus reserve must be less than or equal to the units capacity. The 45-degree line RC in represents this constraint. If the unit can ramp to its maximum within the required timeframe from any initial output level then up to R MW could be provided as reserves. If the response time is very short then this limits the extent to which the unit can ramp up and hence the reserves it can contribute. This is represented by a 'cap' on the reserves provided which creates the region AR'DC.

Co-optimization and the Price of Reserve

In the absence of incentives to provide reserves, one can visualize the unit as normally operating along the line AC. When requirements for reserves are considered, the optimal trade-off between energy and reserve provision must be determined. If the unit would have been operating between A and D it could provide reserves up to the R'D level but no more reserves can be supplied so the units operating point would only change if the energy price changed. But, if the unit would have been operating between D' and C, at E say, it could supply some reserves at E but might need to be 'constrained-off' towards D to provide more reserve.

In the first case, the changing energy price would compensate for any change in output. In the second case, the market would at least have to compensate the unit for the profit foregone on the energy market; otherwise the potential provider will have insufficient incentive to provide reserves. If no additional compensation were required to cover, say the cost of operating at lower efficiency to provide reserves, the required compensation is given by the opportunity cost of backing off generation to provide reserves. This is implied by the interaction of the units energy offers, the energy price and the reserve capability curve. In the PLEXOS formulation this compensation will be automatically embodied in the reserves price, which is equal to the dual variable associated with the constraint defining the required quantity of reserves. Every provider of reserves should receive the same price for every unit of reserve and by definition this will at least compensate any individual provider for the cost of their reserves as stated in their offers.

If the energy price were fixed then, as in the energy market, there would be a single marginal provider of reserves who would set the price of reserves for the system and for whom the reserves price would exactly compensate for the cost of the most expensive accepted reserves offer. In reality, the reserves and energy dispatches are determined jointly. Ignoring any other constraints, there will be two truly marginal nodes at which the combined energy and reserves price pair leaves the producer indifferent between producing more or less energy and/or reserves in any combination.

There are two further complicating aspects:

• When a unit is ramping it may have reduced reserve capability. In PLEXOS, generator reserve response is linked to ramping by the property.
• A generator might be able to provide reserve in a one-to-one relationship with spare capacity, and this is handled with the property.

Generators might also provide reserve by running in synchronous condenser mode.

Mutually Exclusive Services

Spare capacity that is selected for use in regulation reserves, and likewise generation for regulation lower services cannot (by default) also contribute to spinning reserve services. PLEXOS enforces this 'mutually exclusive' constraint automatically.

In the case of multiple spinning reserve services e.g. 6-second, and 60-second spinning reserve, the spare capacity on a generator can be used for any of these services i.e. the same megawatt of spare capacity can provide raise response to any number of raise services (except regulation); and likewise the same megawatt of generation can provide lower response to multiple lower services. This default behaviour can be over-ridden with the Mutually Exclusive property.

Dispatchable Loads

Loads ( Purchaser objects) can provide interruptible load reserves. The amount of interruptible load is defined by the Reserve Purchasers interruptible load bid.

Pumped storage generators can also provide dispatchable load reserves. Refer to the property Reserve Generators Max Pump Response for details.

Reserve Duration and Energy Usage

Regulation reserves in particular are regularly utilized, and the energy reserve cooptimization must account for the fuel use (or hydro water usage) that results. This is handled by the Energy Usage property.

In addition, hydro generators must ensure that sufficient potential energy remains in storage to cover reserve they provide. This in effect places a lower bound on storage whenever reserve is provided. This feature is handled via the Duration property.

External Market Trades

The Market class offers a way to model the trading of ancillary services with external markets. Any Reserve object can be associated with a Market with the Reserves membership. Sales and Purchases to/from the Market act as demand/supply of the service and can set the Price for the Reserve.

Reserve Sharing

You may associate any reserve provider ( Generators or Purchasers) with the Reserve regardless of their location. In reality the reserve must be provided through the transmission network. The Sharing Enabled setting toggles on/off consideration of transmission constraints in the provision of the reserves. The additional setting Sharing Losses Enabled controls whether or not transmission losses are also accounted for when delivering the reserve across the network.

For this feature to work on a Reserve object you must:

1. Identify the 'home' Region that a Reserve object applies to by adding a single Region object to the Reserve Regions collection.
2. Set the phase Transmission Detail flag to "Regional"

The latter restriction is required because reserve sharing works only for transportation models and not with the full OPF.

Reserve Cost Allocation

The energy and reserve cooptimization leads to a price for reserve in each dispatch period. Payments are calculated and made to reserve providers: reported as Generators Revenue, and Purchasers Revenue. However, reserve revenues must be matched by an allocation of those costs. How reserve costs are allocated depends on the rules for the market being studied. A number of compatible cost allocation schemes are provided by the simulator. Allocation to generators is done to those in the Generator Cost Allocation collection.

Reserve Pricing

The required compensation for ancillary services provision is automatically embodied in the reserve's price. Every provider of reserve receives the same price for every unit of reserve and by definition this will at least compensate any individual provider for the cost of their reserves as stated in their energy and reserve offers. If the energy price were fixed then, as in the energy market, there would be a single marginal provider of reserves who would set the price of reserves for the system and for whom the reserves price would exactly compensate for the cost of the most expensive accepted reserves offer. In reality, the reserves and energy dispatches are determined jointly. Ignoring any other constraints, there will be two truly marginal nodes at which the combined energy and reserves price pair leaves the producer indifferent between producing more or less energy and / or reserves in any combination.

Therefore, it is not necessary to define specific offers for reserve, because the reserve price calculated by the cooptimization method will naturally compensate any provider for their opportunity cost. However, PLEXOS allows for reserve providers to charge a premium (above opportunity cost) for providing reserve. The premium is expressed in a multi-band .

The property can be set if a generator must provide a certain amount of reserve regardless of the economics of the dispatch. Note that setting this property does not force the unit to commit, it is only enforced if the unit is operating.

Reserve Markets and Portfolio Optimization

This topic has introduced energy reserve cooptimization in the context of a system-wide reserve requirement. PLEXOS also supports modelling external reserve markets and will optimize trading in both forward and real-time ancillary service markets. See the Market class for more details.

Constraints

The Constraint class provides a number of properties that allow the creation of generic constraints related to both reserve provision and risk.

Reporting

A comprehensive range of output data are provided from the energy reserve cooptimization:

• How much reserve is required in each simulation period ( Risk).
• What price and hence cost was imposed by reserve ( Price, Cost)
• Which generators and / or interruptible load provide reserves: Provision, and Provision.
• How reserve costs were allocated to generators ( Cost)
• What reserve revenues and cost flowed back to companies ( Company Net Reserves Revenue).

References

# G. R. Drayton (1997). Coordinating Energy and Reserves in a Wholesale Electricity Market. Ph. D Thesis. University of Canterbury, Christchurch, New Zealand.