Concise Modelling Guide

Introduction
Intended Functions
How PLEXOS Works
Load and Transmission
1. Load
2. Transmission Network
Generators
Reserves/ Ancillary Services
Emissions
Physical Contracts
Companies, Financial Contracts and Imperfect Competition
Generic Constraints
Decision Variables

This chapter introduces the PLEXOS® simulation software. It describes key concepts, the data structures, its dynamic formulation engine, the type of output produced, and the ways in which the tool can be used to solve real-world problems.

PLEXOS is a simulation tool based on optimization. There are practically no limits to the application of the optimization and simulation approach in this environment, and PLEXOS provides very broad modelling capabilities out-of-the-box. Its object-oriented design makes it easy to learn and use these features, and extend the feature set as required.

Who Should Use it?

PLEXOS addresses many of the limitations of traditional simulation tools by:

using a mathematical programming framework just as is used to clear energy markets worldwide
utilizing the latest algorithms in mathematical programming
calculating unit commitment and economic dispatch and pricing solutions that are mathematically consistent
to the maximum extent possible, co-optimizing decisions such as energy, ancillary services and gas production
offering mathematically robust, auditable and justifiable results: all results are derived from the solution to a set of known equations
using an intelligent formulation engine that adapts the mathematical model to the problem data dynamically
applying optimization across multiple timeframes in an integrated manner so that a single interval's results reflects short, medium, and long-term constraints and objectives
tightly integrating stochastic modelling and optimization across the entire framework

What is it Used For?

The following is a list of examples of how PLEXOS can be used:

Determining the optimal size and timing of new investments in electric generation, transmission and gas infrastructure
Performing cost-benefit and market benefit analysis for transmission and generation assets
Assessing the impact of high penetration of renewable generation sources such as wind and solar on the incumbent generation system and electrical grid
Calculating market price outcomes that account for both fixed and variable cost components and/or game theoretic behaviour
Calculating optimal trading strategies for a portfolio of generation and transmission assets
Valuing generation and transmission assets including complex mixed hydro-thermal systems
Developing chronological load forecast series based on historical load shapes and projected growth in peak and energy
Projecting pool prices under various scenarios of load growth and new builds
Simulating transmission flows in large-scale AC power networks
Calculating nodal prices and their energy, congestion, and marginal loss components
Determining the impact of market design decisions, and rule changes
Projecting short, medium, and long-term capacity adequacy and system reliability
Calculating stranded-asset cost
Analyzing generation and transmission constraints and calculating rentals
Assessing the impact of security-of-supply constraints, and environmental constraints
Optimizing the timing and duration of maintenance outages
Assessing the impact of emissions limits
Optimizing hydro operation with respect to uncertainty
Performing stochastic unit commitment of a portfolio or generators under uncertainty in forecast load, wind generation or electric price
Determining the optimal set of energy contracts (generation and load) that should be purchased
Fuel budgeting and procurement planning
Assessing the adequacy of the gas network to supply gas demands both native and electric

PLEXOS can also be used as a real-time dispatch or ex-ante or ex-post market-clearing engine or to audit the operation of other market-clearing engines and simulation software. Perhaps the most powerful aspect of the tool is that it provides genuine rapid-model-development, dramatically cutting the time and cost of developing and maintaining a power market simulation tool.

What are the System Requirements?

The PLEXOS software requires:

Microsoft Windows (Version 5 or later) 32-big or 64-bit versions
Microsoft .NET Framework

The PLEXOS simulation can also run on Linux.

PLEXOS allows the energy system, consisting of electric and gas parts, to be described as a set of objects that belong to collections, and define various properties. The classes, how they are formed into collections and store properties is described in this section.

An electric and/or gas system model is stored in a database file ("file") in XML format. The PLEXOS graphical user interface ("GUI") provides all necessary functionality to create, add, edit and remove data from the file. You may work on multiple files at a time, each representing a system. Each file holds information about the system in the form of Objects, Memberships and Properties. The GUI is described in the accompanying help articles under the section User Interface Guides, while this article describes the object model and solvers implemented.

A class is a set of rules and definitions about how objects of various classes behave and what data can be defined on those objects. Class behaviour includes what collections objects are allowed to belong to, what collections they must belong to, and how those objects interact with other objects of the same and other types.

The complete list of classes is shown in Table 1 along with a brief description of their function.

Table 1: Classes
Class Group	Class	Description
-	System	The integrated energy system
Electric	Generator	Generating unit, or collection of like generating units
Electric	Fuel	Fuel for a thermal generating unit
Electric	Fuel Contract	Fuel contract
Electric	Emission	Class of generator emission (e.g. NoX, SoX, CO2, etc)
Electric	Abatement	Emission abatement technology
Electric	Storage	Storage reservoir, head-pond, or tail-pond
Electric	Waterway	Waterway for representing rivers, canals, and spillways
Electric	Power Station	Collection of Generators that can be dispatched together
Electric	Physical Contract	Physical contract (import, export, or wheel)
Electric	Purchaser	Demand
Electric	Reserve	Ancillary service
Electric	Battery	Battery energy storage system
Electric	Power2X	Facility to convert electric power to hydrogen and then gas or other products
Electric	Reliability	Reliability group
Electric	Financial Contract	Financial contract (e.g. CfD, swap, cap, etc)
Electric	Cournot	Nash-Cournot game
Electric	RSI	Residual supply index analysis
Transmission	Region	Transmission region/area
Transmission	Pool	Set of transmission regions in a pool
Transmission	Zone	Set of transmission buses in a zone
Transmission	Node	Transmission node/bus
Transmission	Load	Electricity Load
Transmission	Line	Transmission line (AC, DC, or notional/entrepreneurial interconnector)
Transmission	MLF	Marginal loss factor equation
Transmission	Transformer	Voltage transformer
Transmission	Flow Control	Flow control
Transmission	Interface	Transmission interface
Transmission	Contingency	A contingency for use in security constrained economic dispatch
Transmission	Hub	A collection of nodes representing a pricing area
Transmission	Transmission Right	Transmission right (FTR, SRA)
Heat	Heat Plant	Heat production plant
Heat	Heat Node	Heat connection point
Heat	Heat Storage	Storage where thermal energy can be stored and withdrawn
Gas	Gas Field	Field from which gas is extracted
Gas	Gas Plant	Gas processing plant e.g. converting raw natural gas to pipeline quality
Gas	Gas Pipeline	Pipeline for transporting gas
Gas	Gas Node	Connection point in gas network
Gas	Gas Storage	Storage where gas can be injected and extracted
Gas	Gas Demand	Demand for gas
Gas	Gas DSM Program	Demand side management programs
Gas	Gas Basin	Collection of gas fields in a common basin
Gas	Gas Zone	Set of gas nodes
Gas	Gas Contract	Gas contract
Gas	Gas Transport	Gas shipment
Gas	Gas Capacity Release Offer	The release of available pipeline or storage capacity to another party.
Water	Water Plant	Water production plant e.g. desalination plant
Water	Water Pipeline	Water network pipeline
Water	Water Node	Water network node
Water	Water Storage	Water storage tank
Water	Water Demand	Demand for water
Water	Water Zone	Set of water network nodes
Water	Water Pump Station	Collection of Pumps that can be dispatched together
Water	Water Pump	Device to move water upstream using electrical energy
Transport	Vehicle	An electric vehicle (EV, PHEV, etc)
Transport	Charging Station	An electric vehicle charging station
Transport	Fleet	A fleet of vehicles
Ownership	Company	Energy utility or other ownership entity
Universal	Commodity	A commodity that can be produced, consumed, stored, transformed, traded, priced and constrained
Universal	Process	A process that transforms one or more input commodities to one or more output commodities
Universal	Market	A market that can supply and/or demand a Commodity
Universal	Facility	A facility that performs one or more processes
Universal	Maintenance	A class of maintenance events to be optimally placed in time
Universal	Flow Network	A network that flows a Commodity
Universal	Flow Node	A node in a flow network
Universal	Flow Path	A path in a flow network
Universal	Entity	Ownership and/or strategic entity
Generic	Constraint	Generic constraint
Generic	Objective	Generic objective function
Generic	Decision Variable	Generic decision variable
Generic	Nonlinear Constraint	Generic non-linear constraint
Data	Data File	Reference to an external text file
Data	Variable	Stochastic variable
Data	Timeslice	Timeslice for applying to data and/or reporting
Data	Global	Data that are global to the simulation
Data	Scenario	Data scenario
Data	Weather Station	Collection of all weather events related to local station
Execute	Model	Collection of data scenarios that define a model to be evaluated
Execute	Project	Collection of models saved into single project database
Simulation	Horizon	Simulation horizon
Simulation	Report	Set of report selections
Settings	Stochastic	Stochastic settings
Simulation	LT Plan	LT Plan simulation phase
Simulation	PASA	PASA simulation phase
Simulation	MT Schedule	MT Schedule simulation phase
Simulation	ST Schedule	ST Schedule simulation phase
Settings	Transmission	Transmission settings
Settings	Production	Production settings
Settings	Competition	Competition settings
Settings	Performance	Performance settings
Settings	Diagnostic	Diagnostic settings
List	List	Generic list of objects

A file describes a single System object, which represents the energy system or market being studied. This is the root object to which all other objects belong. The System object has a set of collections, one for each class of object in Table 1. All other objects belong primarily to these System collections e.g. Generators, Fuels, Storage, etc. For example, to define a generator, one would add a new Generator object and this gets added to the System collection automatically. When you add an object to a collection, it is called creating a membership.

The collection concept goes further however, because every object you create has collections itself. These additional collections are used to define the relationships that exist between objects in the system. For example, to represent the ownership of a Generator by a Company, one would add the Company object to the companies collection of the Generator object, or vice versa.

Note

What is recorded in the database is the link between the two objects. Referential integrity in the database system automatically deals with deleting memberships of an object if you delete the object itself. Likewise if you rename the object, the memberships are updated automatically.

Table 2 shows some other frequently used relationships, and how they are represented as memberships to object collections:

Table 2: Example Collections
Relationship	Membership
Generator "Big CCGT" connects to the network at point "Big Town 220kV"	Node "Big Town 220kV" belongs to the Nodes collection of Generator object "Big CCGT"
Generator "Little Coal" uses Fuel "Coal"	Fuel object "Coal" belongs to the Generator "Little Coal" Fuels collection
Transmission line A-B flows between nodes "a" and "B"	Node object "A" belongs to the Node From collection of Line"A-B" and Node "B" to the Node To collection

The Parent Class, Child Class, and Collection fields together define a unique type of collection. Parent Name and Child Name define a membership to a collection. All memberships are specified this way, making it easy to write scripts that write these memberships automatically or to paste lists of memberships into a file. For example, the second example in Table 2 can be written with the following five fields:

Parent Class = Generator
Child Class = Fuel
Collection = Fuels
Parent Name = "Little Coal"
Child Name = "Coal"

There are two types of properties:

Attributes: Static values associated with objects
Properties: Static/ dynamic values associated with memberships

NOTE

The term static, refers to values that do not change across time whereas dynamic means they either change by time or in other ways dynamically.

In the database schema, attributes are stored on the objects, but all properties are stored on memberships, and not on the objects; and therefore are identified properties by the five membership fields plus (at least) Property and Value. Depending on whether the property is a static value or a dynamic value there can be other optional fields related to dates, patterns, scenarios, etc. These are described in the chapter help User Interface Guides section.

Most data are stored on objects as members of the System collections. For example, the number of units at a generating station is stored as a property called Units for the Generator object in the System Generators collection. Some data, however, are stored on memberships to other objects collections. For example, the maximum amount of spinning reserve that can be provided by a generator is stored as the Max Response|Max Response property on the membership of the Generator object to the Reserve Generators collection i.e. a membership involving two non-System objects.

The graphical user interface (GUI) largely disguises this underlying data schema, meaning that system-level properties like Generator Units behave like simple data on the object itself i.e. the System object and memberships are essentially hidden and dealt with automatically by the GUI.

The Key Property

Most classes have a key property which indicates if the object 'exists' or not. For example Node class has the property Units which defaults to one, but when set to zero in data excludes the node from the simulation. "Units" is common to many classes, but Table 3 lists all the key properties.

Class	Property	Default Value	Validation Rule	Description
Generator	Units	0	>=0	Number of installed units
Abatement	Units	1	In (0,1)	Flag if emission abatement technology is installed
Storage	Units	1	In (0,1)	Flag if storage is in service
Power Station	Is Enabled	-1	In (0,-1)	Flag if the Power Station is enabled
Physical Contract	Units	1	In (0,1)	Flag if the Physical Contract is in service
Purchaser	Units	1	In (0.1)	Flag if the Purchaser is in service
Reserve	Is Enabled	-1	In (0,-1)	Flag if the reserve is enabled
Market	Units	1	In (0,1)	Flag if the Market is in service
Gas Field	Units	1	In (0,1)	Flag if Gas Field is in service
Gas Node	Units	1	In (0,1)	Flag if the Gas Node is in service
Region	Units	1	In (0,1)	Flag if the Region is in service
Node	Units	1	In (0,1)	Flag if Node is in service
Line	Units	1	In (0,1)	Flag if the Line is in service
Transformer	Units	1	In (0,1)	Flag if Transformer is in service
Flow Control	Units	1	In (0,1)	Flag if the Flow Control is in service
Interface	Units	1	In (0,1)	Flag if Interface is in service
Contingency	Is Enabled	0	In (0,-1)	If the contingency is enabled
Decision Variable	Objective Function Coefficient	0	-	Objective function value of the generic decision variable

There are a large number of classes and across them all a very large number of input properties (more than 1500 in total). To help manage this the graphical user interface uses a Configuration editor. When you create a new input file only a small number of commonly used classes, collections and properties are enabled. Use the Configuration tool to enable more features as you need them.

Many collections such as Generator Fuels can contain more than one object e.g.for multi-fueled generators. However, to keep things simple most collections start off being one-to-one. You must use the Configuration to change them to one-to-many before you add multiple members.

Finally, you may want to define multiple bands on some properties such as Generator Heat Rate Incr and Load Point. Again, use Configuration to set the number of bands you intend to enter. The GUI will give a visual warning if you try to enter more than the specified number of bands.

At any time in the GUI you can press F1 to obtain help on the class, collection or property selected to learn more about that feature before turning it on.

An input file can hold data to any level of detail. For example, in an electric power system a database could contain only static generation capacities and maintenance schedules suitable for a medium to long-term capacity adequacy study; or it could hold half-hourly data including offers and bids and generator technical constraints for use in a detailed chronological simulation.

What makes PLEXOS so flexible and powerful is that any file can hold any combination of short-term data and medium to long-term data. The user can then chose the type of algorithm or algorithms suitable for the required analysis from a suite of options:

LT Plan

Long Term Plan finds the optimal combination of generation new builds and retirements, AC and DC transmission upgrades (and/or retirements) and gas system upgrades (and/or retirements) that minimizes the net present value of the total system costs over a long-term planning horizon like 20-30 years subject reliability and/or other constraints such as emission limits or prices.

PASA

Projected Assessment of System Adequacy schedules maintenance events such that available generation capacity is optimally shared between interconnected regions. It is also a model of discrete and distributed maintenance, and random (forced) outage of generators and transmission lines (this part is called Preschedule). PASA can also calculate reliability metrics such as LOLP.

MT Schedule

Medium Term Schedule Medium Term Schedule is a simulation based on a temporal simplification, with choice of partial or full chronology which can include a representation of the generation and transmission system and constraints to a level of detail the user desires. It is able to simulate over long horizons and large systems in a short execution time. Its results can be used stand-alone or, more importantly, to decompose medium-term constraints, objectives and hydro release policies so that they can be properly accounted for in the full chronological simulation ST Schedule.

ST Schedule

Short Term Schedule is a fully-featured chronological unit commitment and economic dispatch (UCED) model based on mixed-integer programming. It is able to resolve time periods as short as one minute and model the full detail of the electric and gas systems.

These tools have value as stand-alone applications, but their real power is in their integration. Full and automatic integration of these tools (or simulation phases) is provided. For example, the user may choose to run PASA, MT Schedule and ST Schedule in sequence. In this case PLEXOS will feed information from one process to the next as shown in Figure 1.

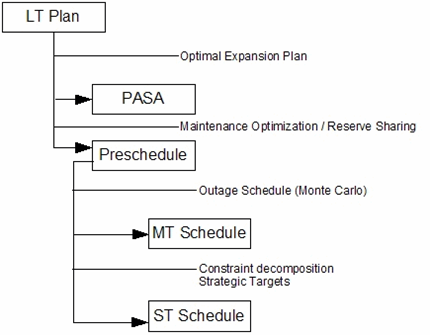Figure 1: Integration of simulation phases

Capacity expansion is implemented via the LT Plan simulation phase. The purpose of the LT Plan is then to solve the capacity expansion problem over the planning horizon: typically expected to be in the range of 10 to 30 years, though any horizon is possible. LT Plan appropriately deals with discounting and end-year effects.

The following types of expansion/ retirement and features are supported:

Building new generating plant
Retiring existing generating plant
Multi-stage projects
Building or retiring AC and DC transmission lines
Multi-stage transmission projects
Expanding the capacity on existing transmission interfaces
Taking up new physical generation contracts
Taking up new physical load contracts
Developing gas fields and pipelines
Developing gas storage
Co-optimizing electric and gas expansion decisions
Deterministic or stochastic optimization

Refer to the article Long Term Planning for more details.

These aspects are handled by the PASA simulation phase

PASA supports three outage types:

Maintenance events that are known in advance

Maintenance events generated by the simulator

Unexpected outages generated by the simulator

NOTE:Transmission Node objects can also be added/ removed dynamically during the simulation with the units property.

Discrete maintenance

Discrete maintenance events represents planned outages, such as major thermal boiler repairs, or regular outages, whose timing and during are known. Data defining these outages is defined as properties for Generator objects with the units out property (and similarly for line and gas pipeline.

Distributed maintenance

Distributed maintenance represents regular outages that are part of the normal maintenance schedule for the unit but for which the timing is not known a priori. PASA can time these outages; taking into account discrete maintenance by balancing regional capacity reserves over an annual timeframe.

Forced outage

Forced outages are those random outages that occur during the normal operation of the generating units or transmission lines. The simulator will generate random outages according to the properties Generator forced outage rate and mean time to repair (and similarly for line and gas pipeline).

Outage duration

PLEXOS supports the definition of outage duration functions for each generator or line in any of these alternative distributions: Fixed duration, uniform, triangular, exponential, weibull, lognormal, SEV, LEV.

Outage severity

Outages may be full e.g. whole generating unit outages are partial e.g. interconnector derating or partial thermal derating. Please refer to the article Maintenance Scheduling for more information.

Maintenance timing

PASA optimizes the timing of maintenance events such that regional/zonal capacity reserves are levelised accounting for the sharing of capacity between regions/zones via the transmission network.

Reliability statistics

PASA calculates the standard reliability statistics such as LOLP, LOLE, EENS and EDNS.

Sampling and convergence

PASA supports both standard Monte Carlo and Convergent Monte Carlo techniques. The latter is used to reduce the number of samples of random outages modelled to obtain a level of convergence.

MT Schedule can be executed stand-alone or run in concert with the other models as in Figure 1. In stand-alone mode MT Schedule can be used to give fast for medium to long-term studies. When run as a component its results are automatically linked to the ST Schedule so that the impact of constraints such as energy limits and storage targets can be correctly accounted for in the short-term schedule.

The MT Schedule handles all user-defined constraints including those that span several weeks, moths or years. This might include:

Fuel off-take commitments e.g. gas take-or-pay contracts
Energy limits
Long-term storage management taking into account inflow uncertainty
Emission quota

Each constraint is optimized over its original timeframe and the MT Schedule to ST Schedule Bridge algorithm converts the solution obtained, e.g. a storage trajectory, to targets or allocations for use in the shorter step of ST Schedule.

Chronology

MTSchedule offers a number of options for reducing the temporal detail. This is controlled by the Chronology.

Under "Partial" chronology each day, week, or month is defined by set of load (or price) duration curves (LDC) each with a number of blocks. The blocks are designed with more details in peak and off-peak load times and less in average load conditions, thus preserving some of the original volatility, although there a multiple slicing methods available.

The simulator schedules generation to meet the load and/or clear offers and bids inside these discrete blocks. All system constraints are applied, except those that deal with generator unit commitment and other intertemporal constraints that imply a chronological relationship between intervals. Chronological is preserved between LDC though i.e. between day or week or month depending on the settings for MT Schedule.

The LDC approach maintains consistency of inter-regional load profiles, ensuring that coincident peaks are captured.

Under "Fitted" or "Sampled" chronology options, unit commitment and other intertemporal details such as ramp constraints are preserved giving a more accurate simulation at the cost of additional computation time. .

Models of Competition

MT Schedule can model competitive behaviour of portfolios over the medium term. This can be 'simply' recovery of fixed costs (LRMC), or more sophisticated game-theoretic behaviours like Nash-Cournot competition.

ST Schedule is a full chronological model i.e. it solves the actual market interval time steps (of any length e.g. 5 minutes, half-hour, or hour) over a horizon from one interval to many years.

Some example uses of ST Schedule are:

A market-clearing dispatch and pricing problem based on generator offers and load bids
A large scale transmission study
A traditional thermal unit commitment and coordination problem
Portfolio optimization
Stochastic unit commitment

ST Schedule generally executes in steps spanning a number of days or weeks, and receives information from MT Schedule that allows it to correctly handle long-run constraints in this shorter time frame.

PLEXOS provides comprehensive stochastic modelling and optimization capabilities and this applies across all simulation phases from LT Plan through to ST Schedule. There are two distinct types of stochastic inputs:

Outages (either planned or unplanned)
random variables (either user-defined samples or synthetic samples generated by the simulator)

Outage Patterns

Outage-related input properties are described in the Forced outage and maintenance section.

The number of outages patterns generated is controlled by the Stochastic Outage Pattern Count setting. Each simulation phase has a Stochastic Method setting that controls how these multiple patterns are simulated. Setting this control to "Independent Samples" (either sequential or parallel variations) invokes the Monte Carlo simulation mode, whereby the simulation is repeated for each outage pattern. Results are produced for each 'sample' and various settings of the Report object control the extend of reporting for the samples and statistics.

Variables

The Variable class is a powerful tool for creating randomized sample data for a wide range of inputs. In fact, practically any input property can be randomized through the Variable class. Some commonly used examples are load, wind, solar, hydro inflows, fuel and electric prices. A Variable object can be used to read either user-defined sample data or to automatically generate sample data during the simulation based on user-defined parameters of the probability distribution.

The number of samples simulated is controlled by the Stochastic Risk Sample Count setting.

The stochastic mode by simulation phase and reporting of samples and statistics for simulation outputs is controlled in the same manner as for a multiple outage pattern run.

Stochastic Optimization

The Stochastic Method setting, which is found on each simulation phase separately, includes a stochastic optimization mode called "Scenario-wise Decomposition". This mode is different from Monte Carlo simulation in that it overcomes the perfect foresight assumption of running independent samples and seeks a set of non-anticipative decisions for user-identified decisions such as unit commitment or hydro release policies. See the article Unit Commitment for more details.

Advanced features are available to model imperfect competition and thus produce market price outcomes that reflect real market behaviour.

Company Class of Objects

The concept of ownership is supported of generation, purchaser, physical, financial and fuel contracts, market transactions and transmission assets through the Company class of objects.

Contract Settlement

Difference payments are calculated on contracts for differences (CFD) and other contracts such as one-ways. Settlement residues (transmission congestion rents) are also reported.

Allocation and Recovery of Fixed Costs

Company class represents common ownership, and hence a model of the underlying market structure and level of competitiveness. The Company article provides references to the oligopoly modelling features, which can be used to set generator pricing options, and control recovery of fixed costs, and perform market power analysis.

PLEXOS is tightly integrated with a number of commercial and academic solvers including the best and fastest commercial mathematical programming solvers available:

CPLEX
Gurobi (Preferred)
MOSEK

In addition the "free for research" edition of PLEXOS integrates open-source solvers: SoPlex/SCIP LP/MIP and GLPK.

When you license PLEXOS you can choose any or all of these solvers as the engine that PLEXOS uses to solve the linear, quadratic, and mixed integer programming problems representing the simulation task.

Detailed outputs is derived from the solution of the various simulation phases. All output properties are described in the Class Reference section, and the report options under the Report topic.

The software architecture of PLEXOS is illustrated in Figure 2:

Data are input to a database via the PLEXOS graphical user interface.
Database entries may refer to text files for data series e.g. load forecasts.
The simulation engine reads the database, extracting the data selected for the current simulation, executes, and produces one or more solution databases and/or text files.
Solution databases can be queried/browsed via the GUI or automatically using the COM or .NET libraries.

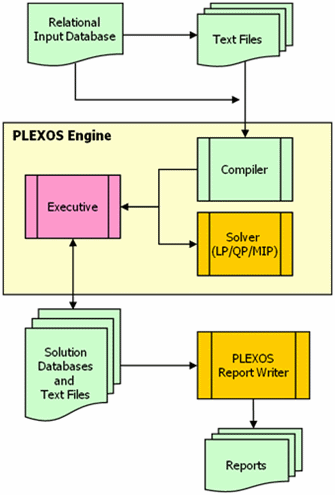Figure 2:Program Architecture

The simulation engine has the layout shown in Figure 3: the key points are:

Written entirely in the Microsoft .NET framework;
It seamlessly integrates: data collection; mathematical program formulation and solution via the integrated solvers; and solution retrieval;
The unique "AMMO" component inside the engine implements the dynamic formulation engine.
Formulation adapts to problem data;
Problem size is minimized;
Execution speed is maximized;
Single code base supports multiple applications; and
No preset limits on problem size; or simulation functionality.

Note

AMMO performs a similar role in PLEXOS as other mathematical languages such as AIMMS, AMPL, or GAMS but is written exclusively for PLEXOS.

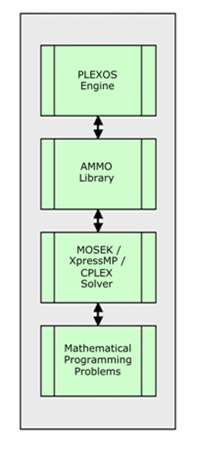Figure 3: PLEXOS Engine Layout

As described earlier, PLEXOS is constructed around an Object Model. That model defines a set of classes, a hierarchy, and rules about how objects interact and relate to each other. Each input file implements the Object Model.

The model is based around three basic elements:

Object
Memberships (also called "relationships"); and
Properties (the data)

All features are accessible through this object model. The PLEXOS interface makes it easy to navigate and edit data in the Object Model.

This chapter describes how load and transmission is represented. It gives a brief introduction to the Region, Zone, Node, and Line classes. We assume that loads are entered as fixed quantities: for loading bidding refer to the Purchaser class.

You can think of Region objects as representing transmission "areas". Zone objects can be either subsets or supersets of Region, and load can be defined at either the Region or Zone level or both.

Node is the connection point for objects such as Generator and no matter how load is defined it will be distributed to Node objects in the simulation.

Loads can be defined either in aggregate on Region and/or Zone objects, or at individual network nodes using Node objects.

When modelling the electric system, your input file must define at least one object. If this is all your model requires then no further data are needed. Implicitly the simulator will include a Node object and place it in that Region so that all load defined on the Region is occur at the Node. This feature is for the convenience for users that do not wish to create a transmission network representation.

If you need to model more than one Region or Node you will need to enable the Node class via Configuration. Once the Node class is enabled you associate each object with a Region via the Node Region membership.

If you are modelling only regional level transmission (with no transmission detail inside the regions) then create one Node per Region and define the load on the Region objects.

Inside any Region you can create multiple nodes to model an AC network in detail. Each Node must be associated only with one Region using the Node Region membership. Nodes may also have a Zone membership. The load can then be defined on the Region and/or Zone and distributed to the nodes using the Node Load Participation Factor property; or alternatively you can define the load directly on the nodes using Node Load.

You may also associate a Zone with a Region via the Zone Region membership and distribute the Region Load with the Zone Load Participation Factor.

Regions are also used to define areas in which maintenance outages should be "optimized" in order to equalize reserves. They also affect certain unit commitment methods such as the "Rounded Relaxation".

Creating a Region and Node Representation

The relationship between the system being modelled and the Region objects in a PLEXOS file depends on the structure of the market. For example, in modelling the:

Australian NEM, a region represents each state;
New Zealand NZEM each island is a region;
Californian market each transmission area is a region;
European continent each country is a region.

To build the required representation, first create the Region and Node objects. Then for each Node, add the Region it belongs in to its Region collection you can create the complement instead by adding the Node to the Nodes collection. This relationship means that the Node will acquire load information from that Region (and vice versa), and be included in that region's summary of load, generation, price, etc.

Regions need to report an energy price from the market. In systems with multiple nodes per region the default is to report a load-weighted average price. This behaviour can be changed using the Design class of objects.

Load data are usually read from text files, the required format for which is described in the article Text File Formats. The Region or Node Load property then points to that text file via the Data File field in the dynamic property grid. The file must contain a header row. The most common format to use is referred to as "Periods in Columns" format:

The first three columns set the year, month, and a day;
The remaining columns hold load figures for each interval of the day;

Each text file contains the interval-by-interval loads for one region only unless you add a Name field as the first field in the file containing the names of the Region objects the load pertains to.

Regions are not required to define load if there is no load in a particular region. Refer to the Text File Formats article for information on other file formats.

Example 1: Load values are read from a CSV format file

Property	Value	Unit	Data File
Load	0	-	North.csv

Figure 4: Example CSV file

Example 2: Loads are defined using a pattern and scaling factors

Property	Value	Unit	Date From	Timeslice
Load	90	-	-	H01
Load	74,47	-	-	H02
Load	60	-	-	H03
Load	47.57	-	-	H04
Load	38.04	-	-	H05
Load	32.04	-	-	H06
Load	30	-	-	H07
Load	32.04	-	-	H08
Load	38.04	-	-	H09
Load	47.57	-	-	H10
Load	60	-	-	H11
Load	74.47	-	-	H12
Load	90	-	-	H13
Load	105.53	-	-	H14
Load	120	-	-	H15
Load	132.43	-	-	H16
Load	141.96	-	-	H17
Load	147.96	-	-	H18
Load	150	-	-	H19
Load	147.96	-	-	H20
Load	141.96	-	-	H21
Load	132.43	-	-	H22
Load	120	-	-	H23
Load	105.53	-	-	H24
Load Scalar	1	-	-	-
Load Scalar	1.1	-	1/01/2010	-
Load Scalar	1.21	-	1/01/2011	-
Load Scalar	1.33	-	1/01/2012	-

Reconciling the Units of Load and Dispatch

It is important that the load data are consistent with the generation and load representation. There are two settings that affect the load formulation:

If the load entered is 'sent out' (net of station auxiliary loads)then you should set the attribute Region Load Metering Point = "Sent out"; otherwise accept the default of "Generator Terminal".
If the input load includes transmission losses that will also be modelled by PLEXOS you should set Region Load Includes Losses = True; otherwise accept the default of False.

For example, in the Australian NEM, forecasts of load are made of the total consumption in the state with imports and exports measured at region boundaries (gross), but energy forecasts are made on a 'sent-out' (net) basis. You should be very careful about what figures you are using and make sure your input and options match each other.

Distribution of Load in a Multi-node Region

The proportion of the total regional load that is placed on each node is based on Node [Load Participation Factor]. The default value of this property is:

One if the region has only one node;
Zero if the region has more than one node.

Therefore in a multi-node region, it is important to set these factors at each load node; but you do not need to set it for non-load nodes.

Creating Input Load Profiles

Refer to the article Load Forecasting

The transmission network is defined using Node and Line objects (and for more advanced use Transformer, Flow Control objects). A Node represents a busbar in the transmission network, and a Line can represent any type of transmission line (AC or DC). Because Lines are an abstract object they can represent a single line or notional interconnector alike.

Lines require two memberships: a Node in their Node From collection and one in their Node To collection: the nodes cannot be the same. An example is given in Figure 5. Here the Line "DE-NL" flows from Node "DE CP" to Node "NL CP".

The reference direction for the line defines what is meant by positive versus negative flows. In this example if the line has a positive flow it is flowing from "DE CP" to "NL CP". The limit in the reference direction is set by the Line Max Flow property, while the limit in the counter reference-direction is set by Min Flow as in Table 4. Note carefully the sign of the minimum flow limits (negative by convention), and also that you do not need to define Min Flow as it will default to the negative of Max Flow.

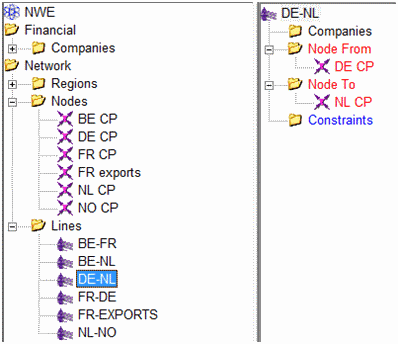Figure 5: Example Line Configuration

Table 4: Line limits

Name	Property	Value	Unit
DE-NL	Max Flow	2100	MW
DE-NL	Max Flow	-3000	MW

Loss Functions

The linearized DC-OPF method that computes transmission AC network flows fundamentally assumes resistance is zero and all voltages are 1 pu. However the formulation used here can incorporate losses as an extension of the standard DC-OPF method. In addition, losses can always be modelled on DC lines and when approximating the network as a transportation model.

You have three options for considering losses in the transmission network and these are (in order of complexity/accuracy):

Ignore losses in dispatch and pricing and simply report the losses that would occur. This is achieved by defining the loss parameters on Line objects (as below) and setting Transmission Losses Enabled = False.
Model only the marginal (pricing) effect of losses by defining the transmission loss factors (TLF) through the Generator Marginal Loss Factor property.
Model losses in dispatch and pricing with Transmission Losses Enabled = True.

Line losses can be specified in one of two ways:

Using the Line Resistance property; or
Defining a custom quadratic function: using the Loss Base, Loss Incr, and Loss Incr 2 properties (reference direction), and (optionally) Loss Base Back, Loss Incr Back, and Loss Incr 2 Back properties (counter reference direction).

Losses on Transformer are defined with the Resistance property.

Note

The default MVA Base for input of Line Resistance is 100 MVA. There are a number of algorithmic options for handling losses and these are described in the article Loss Modelling. The default settings work well for regional modelling.

Optimal Power Flow

As mentioned above, optimal power flows in the AC network can be computed using a linearized DC load flow model with integrated losses. The OPF is co-optimized with unit commitment and dispatch.

A transmission line is considered AC if it defines Line Reactance (or alternatively Susceptance). Any number of disjoint AC networks can be modelled and the OPF is computed in each. Lines and nodes going in/out of service mid-simulation either for planned or random outages can also be handled.

The Transmission object includes many controls for transmission modelling. Several of these options refer to the voltage transmission elements. Thus it is useful to set Node Voltage to identify the voltage level of nodes and connecting lines.

For the linearized DC-OPF there are two distinct formulations available, and these are described in the articles Linearized DC OPF and Loss Modelling.

Contingencies

Any number of contingencies can be defined. The simplest way is to set Transmission N-1 Contingency Voltage Threshold and n-1 will be modelled automatically. Finer control and multi-element contingencies can be defined with Contingency objects.

This chapter introduces the Generator class. A Generator object may be used to represent any of the following in any combination:

A market participant that offers generation to the market
A single generating unit
A generating station with multiple units
A thermal generator that uses various fuels
A component of a combined-cycle (CCGT) plant
A combined heat-and-power (CHP) plant
A hydro generator that draws water from a storage, passing it to another storage and/ or pumps water from one storage to another
A wind generator
Other renewables such as solar
A controllable load (so-called 'anti-generator')

Note that the purchaser class mirrors much of the generator class functionality but for dispatchable load rather than generation.

Generator objects are created in the normal way: see help article User Interface Guide. Like any object in a collection they must have unique names no more than 50 characters in length. The optional Category field can be used to sort the objects into some order other than the default alphabetical order. For example, it might be convenient to sort generators by location and/or type (baseload, intermediate, hydro, and peaking). The pop-up menu Categorize command is used to define these categories.

Units and Capacity

The Generator Units and Max Capacity properties must be defined before the generator can be considered available i.e. the generator is available when the Units property is set to a non-zero value and there is some non-zero capacity. The Max Capacity property defines the size of the units in megawatts.

If the generator is not installed until after the start of the planning horizon, it is sufficient to set the Date From field in the generators Units property as in the following example. It will be assumed prior to this that zero units are installed.

Example: Generator Units and Max Capacity properties

Property	Value	Units	Date From
Units	1	-	1/01/2012
Max Capacity	150	MW	-

As with any property the Units property can be labelled with a Scenario allowing the evaluation of different generator entry scenarios in different Model runs.

If units are decommissioned during the planning horizon, simply add another Units entry with the appropriate date as in the following example.

Example: Decommissioning units

Property	Value	Units	Date From
Units	1	-	-
Units	0	-	1-May-04

Multi-unit Stations

Multi-unit stations are defined exactly like single units, except that the Units property will be set to a value greater that one. The units are assumed to have identical characteristics such as maximum and minimum capacity, heat rate, outage and maintenance rates, etc. In dispatch, all available units are treated identically but may be committed individually. Committed units, however, are assumed to share the total station load evenly between them.

Generators are required to have a Generator Nodes membership (though this is implied if the Node class is disabled). This membership indicates which transmission node the generator injects at. Generators can inject at multiple nodes simultaneously (useful for modelling hydro plant that represent an aggregated chain of plant). In this case you should set the property Generator Nodes Generation Participation Factor to distribute the generation correctly between the multiple nodes.

The Max Capacity value is always the gross generation figure. Auxiliary loads are defined using the properties Aux Fixed, Aux Base, and Aux Incr i.e. they define how the units at the station use power when installed and when operating:

Aux Fixed is the megawatt load drawn by each installed unit at the station. This load is independent of the commit status or load of the unit
Aux Base is the auxiliary loss of a unit at minimum load in MW
Aux Incr is the auxiliary load per unit of load (MW/MW).

Typically the Aux Incr property is used to convert generator terminal (gross) unit ratings to sent-out (net) figures as in the following example, in which the generator is defined with 7% auxiliary losses.

Example: Generator auxiliary losses

Property	Value	Units
Units	4	-
Max Capacity	660	MW
Aux Incr	7	%

Note

See the section Load above regarding the interpretation of the input load figures and make sure that your generator auxiliary loss definition is consistent with the load settings.

Generators consume fuel according to their unit heat rate function expressed in units of GJ/MWh (metric model) or BTU/kWh (Imperial US model). In some modelling situations however, recording fuel use is unnecessary e.g. when using the simulator as an offer and bid clearing engine or for renewable resources that do not consume any fuels per se. In this situation fuel use is assumed zero, and the cost production is determined purely from generator offers or by the variable cost of maintenance (the Generator VO&M Charge property).

In most situations though, the cost of production must be calculated by multiplying the fuel price by the unit heat rate. Three mechanisms are provided for setting the fuel price for a generator and multiple input schemes for specifying the heat rate function of a unit.

Specifying the Fuel Price on the Generator

The simplest way to set the fuel price on a generator is use the Generator Fuel Price property. The advantage of this technique is that it allows there to be a different fuel price on each Generator; the disadvantage is that it may involve repeating information across several generators that use the same fuel.

Fuel Objects

The more common method is to create Fuel objects and associate generators with them using the Generator Fuels] membership. This way you can:

Have multiple generators use the same fuel
Apply constraints on fuel usage
Model fuel-based emissions

If the cost of the fuel varies according to the location of the generator use the Generator Fuels Transport Charge property as a adder to the 'base' Fuel Price.

Gas Network Connection

Connecting a Generator to a Gas Node and simultaneously associating the Generator with a Fuel enables the supply of 'gas' from the gas network to the Generator. The cost of gas is then set by the combination of gas production costs and any charges on the Fuel.

Multi-fueled Units

Generators might be fueled by more than one fuel type e.g. a primary (cheap but limited) and a secondary fuel, or connected to the gas network as well as supplied by another back-up fuel such as liquid fuel. Fuel objects must be used to model this situation. Any number of Fuel objects may be added to the Fuels collection of a Generator. There is no distinction made in the model input between primary and secondary or other fuels. These fuels are used in order of cheapest first, taking into account any constraints on supply of the fuels.

The cheapest fuel will always be used unless a constraint is placed on the offtake of that fuel. Offtake constraints can be defined using the many built-in constraints such as Fuel Max Offtake or for more complex forms using the Constraint class: see section Generic Constraints. Switches between fuels are done automatically according to the implicit values of each available fuel i.e. more expensive fuels will be used at peak times. These fuel trade-offs are fully optimized inside the mathematical formulation resulting in the most efficient possible fuel use.

When the ratios of fuel mixing are fixed, use the Generator Fuels Ratio property to define the fixed ratios. You can also define a penalty for violating the fuel mixing constraints; which is useful when the defined ratios are 'desired' but might be infeasible due to other constraints. Other properties are available to set minimum and maximums input and ratios.

Start Fuels

A Generator object can be defined as using a fuel (or fuels) for starting that are different to its fuels for generating. Adding Fuel objects to the Generator Start Fuels collection establishes this relationship. The amount of fuel used to start the unit is controlled by the property Generator Start Fuels Offtake at Start defined on the membership.

The fuel used to start a unit combines with the Generator Start Cost property to set the total cost of starting a unit.

When using multiple bands of Start Cost to represent hot, warm, cold starts you can also use multiple bands on Generator Start Fuels Offtake at Start.

Run up and down

For hourly resolution modelling it is usually adequate to assume that generators start up and reach Min Stable Level within a dispatch period. For sub-hourly modelling in particular, this assumption might not be valid. In this case use the Generator Generator.Run Up Rate and/or Run Down Rate. More complex forms of these constraints defined with the Start Profile and Shutdown Profile properties.

Definition of the unit heat rate function for thermal generators is supported using one of a number of formats including:

Constant heat rate using Heat Rate or Heat Rate Incr
Incremental heat rates using Heat Rate Incr and Load Pointin multiple bands
Average heat rates using Heat Rate and Load Point in multiple bands
Polynomial function using Heat Rate Base, Heat Rate Incr, Heat Rate Incr 2 and Heat Rate Incr 3

These properties are described in detail in the article Heat Rate Modelling. In the following we describe the common usage of these properties.

The Generator property Heat Rate determines the amount of fuel used per megawatt of generator load i.e. Fuel Offtake = Heat Rate × Generation. In the simplest case, where only the Heat Rate property is defined, a single heat rate will apply across the entire range of generator loads.

Example: Generator with constant heat-rate (metric)

Property	Value	Units
Units	4	-
Max Capacity	660	MW
Fuel Price	1.16	$/GJ
Heat Rate	9.42	GJ/MWh

Example: Generator with constant heat-rate (Imperial US)

Property	Value	Units
Units	4	-
Max Capacity	660	MW
Fuel Price	1.16	$/MMBTU
Heat Rate	9420	BTU/kWh

Heat rate generally varies across a unit's operating range. In this case it is convenient to specify the heat rate at several points. This is done using the Load Point property in combination with Heat Rate (or Heat Rate Incr for incremental rates) as in the following example.

Example: Multi-point heat rate function using average rates (metric)

Property	Value	Units	Band
Units	4	-	1
Max Capacity	660	MW	1
Min Stable Level	264	MW	1
Fuel Price	1.16	GJ/MWh	1
Load Point	264	MW	1
Load Point	660	MW	2
Heat Rate	11	GJ/MWh	1
Heat Rate	9.42	GJ/MWh	2

Note

The Band is used to match the load points with the heat rates. The heat points must be in order or an error will be reported. Note further that the load point values need not match the Min Stable Level and Max Capacity.

If your data is for incremental heat rates, rather than average, then use the Heat Rate Incr property instead of Heat Rate.

An alternative to the load point/heat-rate method is the specification of the properties Heat Rate Base, Heat Rate Incr, Heat Rate Incr 2 and Heat Rate Incr 3. These parameters describe a order-3 polynomial function directly.

Heat Rate Function Verbatim

By default the data provided to define the heat function are used to fit a order-3 polynomial and then a piece-wise linear approximation with Max Heat Rate Tranches number of tranches. You can overrides this behaviour and force the simulator to use your input curve verbatim by setting the Max Heat Rate Tranches equal to the number of load points.

Heat Rate by Fuel

The heat rate function may vary by fuel type used. Fuel-specific heat rate functions can be defined on the properties of the Fuel object inside the Generator Fuels collection. Any settings here override the fuel use function defined on the Generator.

Convexity

The marginal heat rate function should be monotonically non-decreasing unless you set the Production Heat Rate Error Method = "Allow Non-convex". Refer to the article Heat Rate Modelling for details on how the simulator deals with non-convex functions.

Short-run Marginal Cost

The short-run marginal cost of generation at a particular megawatt level is calculated as the fuel price (as defined above) combined with the heat rate function and VO&M Charge i.e.:

SRMC = Fuel Price × Heat Rate Incr + VO&M Charge

Where Heat Rate Incr is derived from the polynomial fit to heat function.

Offers for generation can be used to define capacity and price on their own or to override the short-run marginal cost (SRMC) pricing. Generator offers do not affect the calculated cost of generation, only the prices and quantities offered to the energy market.

Generator offer quantities are assumed to be generator-terminal (gross) values while offer prices are sent-out (net) values.

The properties Offer Quantity and Offer Price define a set of multi-band offers for a generator. Note the following:

Offer Quantity is by default incremental but can be changed to cumulative (like Load Point with the setting Generator Offer Quantity Format
There is no limit to the number of offer bands that can be input but you should use the Configuration form to set the number of bands you want to use
By default the offer bands are cleared lowest to highest in price unless you set the Generator attribute Offers Must Clear in Order
Offers can vary over time using the Date From, Date To, and Timeslice fields, or read from files using the Data File field
Generation offer quantities never override the Max Capacity but if the total quantity offered is less than Min Stable Level that constraint is relaxed to allow generation according to the offers.

Example: Defining a multi-band Offer

Property	Value	Units	Band	Timeslice
Offer Quantity	140	MW	1	-
Offer Quantity	35	MW	2	M1-3,12
Offer Quantity	50	MW	2	M4-11
Offer Price	0	$/MWh	1	-
Offer Price	45	$/MWh	2	-

Note

The number of bands that have been defined on a Generator is allowed to change across the horizon, with inactive bands assumed to have a zero Offer Quantity by default.

Offers on Multi-fueled Units

On multi-fueled units, the generation offer applies to all fuels unless you define the individual offers using Generator Fuels Offer Quantity and Offer Price.

No Load Cost

For electric markets with centralized unit commitment (e.g. Ireland) additional offer data can be defined. Offer No Load Cost is a cost incurred for any hour that a unit is committed.

Balancing market offers

In a balancing market, offers are 'centred' around a base value and the offer is divided in to increment and decrement parts being offers to increase generation from the base and bids to decrease respectively. See the article Balancing Markets for details.

Pumped Storage Bids

Bids can be defined for pumped storage units with the properties Pump Bid Quantity and Pump Bid Price.

A mark-up is a price for generation above marginal cost. Mark-ups might be required to recover fixed costs or semi-fixed costs like Start Cost and no-load cost (see the article Heat Rate Modeling for a definition). The Competition setting No Load Cost Mark-up automatically adds a mark-up that will recover no-load cost.

For manually defined mark-ups, the property Generator Mark-up is the absolute amount that the generation of the unit is marked up above marginal cost. If you prefer a relative mark-up use the property Bid Cost Mark-up and optionally additional Mark-up i.e. the two properties can be used together.

Both properties can be multi-band when used in conjunction with the Load Point properties as in this example:

Example:Mark-up Properties

Property	Value	Units	Band
Bid Cost Markup	0	%	1
Bid Cost Markup	20	%	2
Bid Cost Markup	50	%	3
Bid Cost Markup	120	%	4
Load Point	40	MW	1
Load Point	70	MW	2
Load Point	90	MW	3
Load Point	100	MW	4

In chronological simulation phases (any of LT Plan, MT Schedule and ST Schedule depending on settings) generator unit commitment and economic dispatch (UCED) is optimized using mixed-integer programming. Unit commitment decisions are optimized across each step of the simulation, where the step size is configurable to any length (minutes, hours, days, weeks) and additional look-ahead can be specified. Deterministic, Monte Carlo simulation and stochastic unit commitment functions are available. See the article Unit Commitment for details.

The following table describes the common generator properties related to unit commitment and gives an indication of the difficulty of modelling them in terms of computation time and problem size. You should use this as a guide when determining the most appropriate data for your Generator objects in terms of accuracy versus computation time.

Table 5: Unit commitment related properties

Property	Description	Computational Implications
Min Stable Level	The minimum generation level when the unit is committed	Adds only one additional constraint per generator/period to the formulation. Generally easy for the solver to optimize, unless MSL is a very high proportion of capacity.
Min Up Time	The minimum number of hours that a unit must run for once it has been started	Adds multiple variables and constraints to the formulation. The longer the minimum up time, the more terms are added, so long times can produce a large formulation. These limits are relatively difficult for the solver.
Min Down Time	The minimum number of hours that a unit must be down after it has been shutdown	As above for minimum up time
Start Cost	The cost of starting up a unit	Start cost adds variables and constraints to the formulation. If you define multiple start costs as a function of the number of hours a unit has been down (cold, warm, hot, etc) then additional integer variables are required in the formulation and this can be difficult for the solver to optimize.
Run up Rate or Start Profile	A specific regime of megawatts steps that a unit must run through as it starts up	Adds constraints to the formulation. Start profile is no more difficult than start cost for the solver.
Run Down Rate or Shutdown Profile	A specific regime of megawatts steps that a unit must run through as it shuts down	As above for [Start Profile]

Linear Versus Integer Commitment

By default only the linear relaxation of the unit commitment problem is solved. In the linear relaxation the constraints on minimum stable level, and minimum up and down times will not necessarily be obeyed: because they represent an integer not linear decisions. Start costs will influence the dispatch but not in the same way as they would if the problem were solved as a mixed integer program.

Use the Production Unit Commitment Optimality setting to switch between linear and integer modes. You can also choose this setting by Generator object using the Generator Unit Commitment Optimality property: thus you can decide which generators will be modelled with integer variables and which will remain linear.

Performance of the mixed integer solver is very much a problem-specific characteristic. You should experiment with solving a short horizon, determining by experimentation the best combination of options to use, before attempting to solve the complete horizon.

Note

The Performance class offers a number of tuning parameters for the mixed integer solver and solver-specific settings can be made through Hidden Parameters.

Rounded Relaxation

The linear relaxation to the unit commitment problem is problematic not just because the integer type constraints can be violated but also because the linear start and unit commitment variables can be 'basic' variables and thus affect the shadow prices. More specifically the cost of starts and the no-load cost of generation can affect the market energy prices. In contrast, in an integer solution, the energy price is based on the marginal cost of thermal generation and does not include any 'roll in' of start cost or no-load cost.

Thus we always prefer a integer solution, but solving to optimality using MIP can be time consuming, thus a heuristic unit commitment method called "Rounded Relaxation" ("RR") is available which solves with only a small increase in run time over the linear relaxation. See the article Unit commitment for more details.

Self Commitment Markets

If the system being studied is a self-commitment market, generator offers only include Offer Quantity and Offer Price. From the market clearing engine's viewpoint, generating units can switch on and off as required at no cost, and operate at any level. In this type of markets it is the responsibility of the generators' to structure their offers in a manner that is consistent with constraints on unit operation implied by unit commitment: also see below the use of Fixed Load in this context.

Initial Commitment and Load

In an operational context where the initial commitment state of generators is known you can input this by setting the properties Initial Units Generating and Initial Generation. If you are using minimum up and down constraints you should also define Initial Hours Up and Initial Hours Down.

Example: Unit is initially 'on' and has been up for six hours

Property	Value	Units
Units	1	-
Max Capacity	100	MW
Min Up Time	12	hrs
Min Down Time	8	hrs
Initial Units Generating	1	-
Initial Generation	90	MW
Initial Hours Up	6	hrs
Initial Hours Down	0	hrs

In the above example it is assumed that, at the start of the horizon, the unit is 'on' and must stay on for another six hours to meet its minimum up time.

Several Generator properties are available for modelling restrictions/constraints on the unit commitment and dispatch of generators.

Must-run

Generator Must-Run Units is the number of units at the station that must be committed. It is free to commit more than this number of units, and will only commit less if the units are out-of-service.

Example: Unit must run during peak times on weekdays

Property	Value	Units	Timeslice
Units	1	-	-
Max Capacity	100	MW	-
Must-run Units	1	-	W1-6,H14-19

Pre-defined Commitment Schedule

The Generator property Commit can be used to 'hardwire' generator unit commitment. Commit specifies the number of units that (if available) should be committed. The default value of -1 indicates that the unit commitment should be optimized not pre-determined. Thus Commit can be used in a pattern to indicate times when a certain commitment is needed but left at default for other periods and the simulator will optimize its commitment in those times.

Example: Unit must be committed during weekday peak times and off in the weekend but freely optimized at other times

Property	Value	Units	Timeslice

Minimum and Fixed Unit Load

Generator Min Load sets a minimum unit load level (subject to unit availability). Min Load is sometimes used to model the effect of loads not included in the simulation such as the load implied by heat demand from a combined heat and power unit.

In self-commitment markets (Australia for example) generators can define a 'fixed load' profile for a number of hours. This is used to control the dispatch of the plant by the market during start up and/or shutdown of large relatively inflexible units. The property Fixed Load is provided for this purpose. When Fixed Load is non-zero the generator with dispatch exactly according to those loads, but when Fixed Load is zero the dispatch is optimized. The behaviour of Fixed Load can be changed so that zero values are also enforced using the Generator attribute Fixed Load Method.

Note:

When you define a multi-unit generator, both Min Load and Fixed Load apply to the generating station as a whole, not to individual units.

Energy Limits

Generators can be included in one or more Constraint objects to control their total energy over any period. For example, there may be minimum or maximum energy on a generator over each day, week, month, or year. As a shortcut to using the Constraint class the Generator class includes these energy-related properties:

Example: A generator subject to minimum load and maximum capacity factor (e.g. simple hydro)

Property	Value	Units	Timeslice
Units	1	-	-
Max Capacity	100	MW	-
Min Load	20	MW	M1-5,11-12
Min Load	40	MW	M6-10
Max Capacity Factor Month	40	%	M1-5.11,12
Max Capacity Factor Month	75	%	M6-10

The additional property Generator Energy Scalar is provided so that energy limits defined using the above properties can be easily scaled using a factor. This is useful for introducing volatility into the energy limits by applying a Variable to the Energy Scalar.

Rough Running Ranges

A generator rough running range is a range of load levels that must be avoided. Typically these apply to hydro generators and are load levels that might cause cavitation in the turbines, but you can apply rough running ranges to any Generator. The property Rough Running Point marks the start of a rough running range and Rough Running Range is the length of the range, both properties are in megawatts and can be multi-band to define multiple such ranges.

The Fuel Contract class provides a set of properties for modelling constraints and costs associated with fuel contracts. The Fuel Contract Fuel membership sets up the relationship between the fuel contract at the fuel it applies to. Applying a fuel contract to a fuel replaces the need to define a price on that fuel. It is allowed to apply more than one Fuel Contract to a Fuel, which might then represent different sources for that fuel.

Fuel Contract availability is set by the property Quantity and its hour, day, week, month, and year variations. The price is set by the Fuel Contract Price property. Both Quantity and Price can be multi-band to represent multiple price tiers for supply of the fuel.

Take-or-pay commitments are modelled using Take-or-Pay Quantity again with hour, day, week, month, and year versions. Fuel Contract Take-or-Pay Price sets the penalty price that is paid to avoid the take-or-pay commitment (per unit of fuel).

The article Planned and Random Outages provides a complete guide to the Monte Carlo simulation of random outages and the method of placing maintenance outages in time such that capacity reserves are levelised.

Generator Forced Outage Rate sets the expected level of unplanned outages (annual average) that result in a partial or complete loss of generating capability for a certain period of time. Likewise Maintenance Rate for maintenance outages.

The timing of forced outages is random, but repeatable according to the Model Random Number Seed. Although maintenance timing is guided close to the optimal placement by PASA the timings are subject to some randomization i.e. each sample will have a different maintenance schedule. This is done so that the simulation results across multiple Monte Carlo samples show meaningful variation and the simulation is not biased by a single optimized maintenance schedule.

The duration of each outage event can be either constant (by setting only Mean Time to Repair) or randomized by selecting a distribution type and appropriate inputs. See Generator Repair Time Distribution.

Partial outages can be modelled. The property Generator Outage Rating sets the limit of generator load during each outage event.

Multiple outage types (partial, complete, forced, maintenance) can be defined by using the Band field to separate the definition of different outages.

Example: Using multiple bands for different outage types

Property	Value	Units	Band
Units	1	-	1
Max Capacity	100	MW	1
Forced Outage Rate	7	%	1
Mean Time to Repair	36	hrs	1
Forced Outage Rate	3	%	2
Mean Time to Repair	12	hrs	2
Outage Rating	60	MW	2

Fixed operations and maintenance costs are input in units of currency per kilowatt year e.g. $/kW/year. The annual fixed costs are then based on the installed capacity thus:

FO&M Cost = FO&M Charge × Units × Max Capacity × 1000

Fixed O&M charges are important when optimizing capacity expansion: see the article Long Term Planning.

If you want to account for the annualized fixed costs of existing generators you can input those using Equity Charge and Debt Charge. These charges will add to the total annual fixed costs of the generator.

The dynamic bidding of generation by companies to recover these fixed costs can be modelled. The first step in that process is to make a notional allocation of fixed costs to each interval of the year. The costs are allocated according to the pool revenue the generator earns in each interval i.e. the higher the pool revenue in any given interval, the more fixed costs get allocated to that interval. This allocation is calculated regardless of whether the cost recovery algorithm is 'on' or not. That method is enabled via the Competition Equilibrium Model attribute: see the article LRMC Recovery Algorithm for more details.

CCGT are modelled in one of two ways:

By modelling the individual gas turbines and separate steam turbines each as Generator objects and linking them together using the Generator Heat Input membership
As a single equivalent Generator object with a complex heat rate function

The first approach is described in the article Combined Cycle. In the second approach the heat rate function of the 'equivalent' single generator can be defined using a multi-band Load Point and Heat Rate Incr set, and the function is allowed to be non-convex (meaning the incremental heat rate can go and up down across the range of operation according to the changes in operation mode of the CCGT).

Note

For PLEXOS to optimize with non-convex heat rate functions, you need to set the attribute Production Heat Rate Error Method = "Allow Non-convex".

The CHP modelling feature allows you to:

Represent the impact of increasing heat load on overall fuel consumption (i.e. on electrical efficiency).
Model the ability for two or more Generator objects to deliver heat to a single heat demand point, and hence let the model choose which of the generators to use to meet that heat load.
Model the ability to meet the heat load by heating boilers within a power plant, and to.
Split the fuel offtake reporting into a power and heat component.

See the article Combined Heat and Power

The Generator class models hydro and pumped storage generators. The wide selection of properties available on the Generator class means there are many ways to model hydro as described briefly below and detailed in the Hydro Modelling section starting with the article Hydro Classes.

Hydro as Energy-constrained Generators

Defining a 'simple' generator subject to some minimum generation and maximum energy is the simplest approach to modelling hydro. As described above, the energy limit can be defined using the various period type versions of Max Energy or Max Capacity Factor Factor, and the run-of-river generation by Min Load.

Example: Hydro as energy-constrained Generator

Property	Value	Units	Scenario
Max Energy Week	2	GWh	-
Max Energy Week	1.8	GWh	dry year
Max Energy Week	2.5	GWh	wet year
Min Load	10	MW	-
Min Load	6	MW	dry year
Min Load	13	MW	wet year

Hydro With Storage

A hydro generator with storage is defined by adding a Storage object to the Generator Head Storage collection. The Generator Tail Storage collection is used to create cascading networks of storage and generators. See the article Cascading Hydro Networks for more details.

Hydro Generator Efficiency

Generator Efficiency Base and Efficiency Incr properties sets the relationship between generation and water throughput, although you may also use the normal heat rate properties.

It is important to note that the units of storage default to 'potential energy' not volumes of water. To change this see the article Units of Data.

Example: Hydro efficiency function (metric volume storage model)

Property	Value	Units	Band
Units	1	-	1
Max Capacity	60	MW	1
Load Point	20	MW	1
Load Point	40	MW	2
Load Point	60	MW	3
Efficiency Base	58	cumec	1
Efficiency Incr	0.5	MW/cumec	1
Efficiency Incr	0.48	MW/cumec	2
Efficiency Incr	0.42	MW/cumec	3

For more details on hydro efficiency and head effects see the article Hydro Generator Efficiency and HeadEffects.

Pumped Storage Hydro

The properties Pump Efficiency and Pump Load are provided to define pumped storage hydro. Although pumped storage can be included in a hydro cascade it is most commonly modelled as a 'closed loop' system. The system is defined by setting both a Head Storage and Tail Storage for a Generator as in Figure 6 and then defining at least the properties in the example below.

Figure 6:Pumped Storage Membership

For more details see the article Pumped Storage

Some generators, particularly hydro, can operate in synchronous condenser mode in order to provide fast spinning reserve. The property Generator Sync Cond Units defines the number of units that can operate in this way. This must be a subset of the Units. Generator Sync Cond Load sets the load drawn while operating in this way. Generator Must-run Sync Cond Units allows you to force a number of units to run in synchronous condenser mode, while Sync Cond VO&M Charge defines the additional operations and maintenance costs.

A Generator is a candidate for capacity expansion in LT Plan if its Max Units Built property is defined. The overnight build cost is given by Build Cost in $/kW, which can be multi-band to represent a stream of payments leading up to the opening of the plant. The properties WACC and Economic Life can be defined so that the build cost is converted to an annuity.

Example: Thermal plant for capacity expansion

Property	Value	Units
Units	0	-
Max Capacity	250	MW
Heat Rate	7.9	GJ/MWh
Max Units Built	1	-
Build Cost	1200	$/KW
WACC	12	%
Economic Life	25	years

Retirement candidates have their Max Units Retired property defined. Note that Units is always the number of incumbent units, therefore [Max Units Retired] must be less than or equal to Units plus Max Units Built.

For more details see the article Long Term Planning.

This chapter provides an overview of ancillary services modelling. It is the Reserve class of objects that control this feature.

Each Reserve object has a type attribute which can be set to one of:

A spinning up reserve service provided by units online.

A spinning down reserve service property by units online

A regulation up (frequency keeping or load following) service provided by units online separate to their spinning reserve provision

As for Regulation Raise but this is the 'down' service

Non-spinning reserve provided by units that are not online but that can start quickly

A combination of Raise and Replacement.
The property Reserve Timeframe is the number of seconds that the response is required in. This limits the amount of spinning reserves that generators can provide if they define ramp rate limits and/or start up times. The Duration property is the length of time that the reserve must be sustained for, and affects the amount that can be provided by hydro with storage.

The amount of the service required is set by the combination of:

Reserve Min Provision; and optionally
Reserve Region Load Risk multiplied by the Region Load

The requirement can also be dynamic based on generation and/or transmission flows. The collection Reserve Generator Contingencies defines a list of generators, the maximum load (above the Reserve Cut-off Size) of which sets a reserve requirement. Likewise the Reserve Line Contingencies collection does the same for line flows, though you must define either Reserve Line Contingencies Flow Forward Coefficient or Flow Back Coefficient so it is known what proportion of reference direction or counter flow is 'at risk'. For generator risk you can adjust the proportion of generation at risk using the Reserve Risk Adjustment Factor.

When dynamic risks are included the overall requirement is the maximum of any one of the contingencies and the Min Provision plus region demand risk.

You should set the Reserve VoRs property, which is the shortage cost of reserves, if there is a possibility that the system cannot provide enough of the service.

The collection Reserve Generators defines the list of generators that can provide the service. You must define this set or there will be no generators providing the service. The effectiveness of the spare capacity provided for reserve can be adjusted from it default of one-to-one using the property Reserve Risk Adjustment Factor. Maximum and minimum reserve provision can be set generator-by-generator using Reserve Generators Max Response and Min Spinning Provision respectively.

Generators can provide spinning 'raise' reserve in four ways:

By partially loading units
By running units in synchronous condenser (or "tail-water-depressed" (TWD) mode for hydro units).
By starting quickly enough to provide a response with the Time frame
By reducing PumpLoad

Generators can provide 'lower' reserve in two ways:

By loading units above Min Stable Level
By increasing Pump Load

The Reserve Generators Max Response and Max Sync Cond Response properties define how much reserve a unit can provide from each mode respectively. Max Replacement sets the response limit for replacement reserves, while Max Pump Response sets the limit for pumped storage.

The property Reserve VO&M Charge sets the additional operations and maintenance costs associated with providing reserves, and is charged against all spinning and regulation services.

When a generator is ramping at the time it is called upon to provide spinning reserve its effectiveness is either reduced or enhanced depending on the direction of the service and ramp. For example a generator ramping up is less effective at providing further ramping for spinning reserve up provision. However, generators can usually provide a faster rate of ramp for spinning reserve than they their normal operational ramp rate, thus the property Reserve Generators Response Ratio is provided, which is equal to the ratio of normal ramping rate to emergency ramping.

The property Reserve Energy Usage is the proportion of the reserve provided that will be called upon on average. Generators providing regulation reserve (in particular) will be called upon regularly. This implies that fuel (for thermal) and water (for hydro) generators will be consumed with a certain probability when regulation reserves are provided. Setting this property means that fuel and hydro energy will correctly account for reserve provision.

Reserves are jointly optimized with energy to produce an optimal dispatch and reserve provision with associated energy and reserve pricing. Any number of Reserve objects can be defined and co-optimized.

Reserve can be bought and sold to and from external markets using the Market class of objects.

There are two types of interruptible Load

Pumped storage generators in pump mode that can reduce pumping to provide into the spinning up service.
Loads that can be curtailed to provide spinning up service

Purchaser objects are used to model interruptible load for the purposes of 'raise' type services (spinning reserve but not usually regulation reserve). Add Purchaser objects to the Reserve Purchasers collection to allow those purchasers to provide interruptible load services.

For pumped storage generators, the Pump Load less the Min Pump Load is automatically counted as spinning reserve for 'up' services, but you can set a maximum provision using Reserve Generators Max Pump Response.

The energy and reserve co-optimization results in an endogenous 'price' for the provision of reserve by each generator. There will naturally be one or more marginal generators for energy and one or more for each ancillary service, and the market prices for the ancillary services will naturally emerge from the optimization.

In some markets though, generators and loads can place offer prices on provision of reserves. The properties Reserve Generators Offer Price, Offer Quantity are provided for provision of spinning and regulation and Sync Cond Offer Price for provision of spinning reserve from synchronous condenser mode, and finally Pump Offer Price for the provision of pump interruptible load. These offer prices add to the endogenous price of reserve provision, thus they act as a premium on the service.

This chapter provides an overview of the emission and Abatementclasses.

The Emission class allows you to define any number of emissions. Those emissions can be associated with generation and/or fuel use. Constraints can be placed on emission production across any time period. Because emission production and any prices and/or constraints placed on it is fully integrated into the mathematical programming framework, the generator dispatch and market pricing outcome will correctly reflect the economic impact of emissions.

You might choose to model the emissions as a function of generation and/or a function of fuel depending on the type of emission. In general CO2 is often modelled as a function of generation, whereas SOx (SO and SO2 by products) is best modelled as a function of fuel used. NOx (NO and NO2) is often modelled using a combination of generation and fuel emission properties along with the scaling factor Generator Fuels Emission Scalar: refer to the help on this property for more details.

An Emission object has a Fuels collection, which represents the set of fuels that produce the emission when they are consumed. On this membership, the [Production Rate] property defines the amount of the emission produced per unit of the fuel used. The consumption of the fuel by generators is tracked and the production rate applied to calculate the total emissions produced. The emissions counted will include those from fuel used to start units according to the Generator Start Fuels Offtake at Start property.

An Emission object has a Generators collection, which represents the set of generators that produce the emission either additional to or including those from fuel use. It is on this membership that the property Production Rate is defined, which is the amount of emission produced per megawatt of generation. Note that the property is multi-band meaning that you can combine it with Load Point to define a stepwise marginal emission production function as in the following example:

Example: Generator emissions

Membership	Property	Value	Units	Band
Generator (Big Coal)	Units	1	-	1
Generator (Big Coal)	Max Capacity	600	MW	1
Generator (Big Coal)	Heat Rate	14	GJ/MWh	1
Generator(Big Coal)	Heat Rate	12	GJ/MWh	2
Generator (Big Coal)	Heat Rate	11	GJ/MWh	3
Generator (Big Coal)	Load Point	200	MW	1
Generator (Big Coal)	Load Point	400	MW	2
Generator (Big Coal)	Load Point	600	MW	3
Emission (CO2) Generators (Big Coal)	Max Volume	30	kg/MWh	1
Emission (CO2) Generators (Big Coal)	Max Volume	35	kg/MWh	2
Emission (CO2) Generators (Big Coal)	Max Volume	40	kg/MWh	3

NOTE

that it is not required to provide a multi-band function for emission production. You can use Load Point multi-band to define your heat rate function and input a single band for the emission production rate if preferred.

In addition there can be emissions produced at generator start up and this is set by the Emission Generators Production at Start property.

Generators with emission mitigation technologies can capture some proportion of their emissions and prevent them from being released. The property Emission Generators Removal Rate is the proportion removed. The incremental cost of removal is set by the property Emission Generators Removal Cost. Thus the net emissions production for a generator is given by:

(1 - Removal Rate) x Production Rate x Generation
and this is added to by fuel-based emissions:
(1 - Removal Rate) x Production Rate x Heat Rate x Generation
Here the heat rate is used as a placeholder for the average heat rate in particular generation block.

A more advanced way of modelling emissions abatement is through the use of Abatement objects. Each is associated with a decision variable so that the optimal combination of abatement technologies can be found. See the Abatement topic for more details.

The Emission class provides two price inputs for emissions. The property Emission Price is the 'accounting price' meaning that it is the price used when the cost of emissions is calculated and passed on to the generators and their owning companies. The property Emission Shadow Price is the priced charged inside the optimization, meaning it is the priced used for dispatch and pricing. If you define only one of these properties or your model has constraints on the emissions that imply a shadow price the resulting accounting and shadow prices used are as described in Table 6:

Table 6: Emission price inputs and outputs

Input	-	-	OUTPUT	-
Emission [Price]	Emission [Shadow Price]	Constraint	Price	Shadow Price
Defined	Defined	No	Emission [Price]	Emission [Shadow Price]
Defined	Defined	Yes	Emission[Price]	Constraint Shadow price
Defined	Not Defined	No	Emission [Price]	Emission [Price]
Defined	Not Defined	Yes	Emission [Price]	Constraint shadow price
Not Defined	Defined	No	Emission [Shadow Price]	Emission [Shadow Price]
Not Defined	Defined	Yes	Constraint shadow price	Constraint shadow price
Not Defined	Not Defined	No	Zero	Zero
Not Defined	Not Defined	Yes	Constraint shadow price	Constraint shadow price

Emissions can be included in one or more Constraint objects to control their total production over any period. For example, there may be an emission limits over each day, week, month, or year. As a shortcut to using the Constraint class the Emission class includes the property Max Production with variants for hour/day/week/month/year.

By default these limits are across all emissions represented by the object. You might prefer to limit emissions across a subset of generators or fuels. The Constraint Generators Emission Coefficient and Constraint Fuels Emission Coefficient are provided for this purpose. Note that if your dataset contains more than one emission then the Constraint will need to know which emission or emissions are being referred to by these coefficients. This is done by adding the Emission object into the Constraint Emissions collection with no coefficients set: here it is acting purely as a filter on the emissions from the generator/fuel.

Emission constraints are generally not 'hard' limits, but carry a penalty cost either across all emissions or just for emission above some given threshold. To model this situation use the Constraint Penalty Quantity and Penalty Price properties, which can be multi-band to give a stepwise emission penalty function.

Emissions can be traded from/to an external market using a Market object. This might represent the option for a generator to purchase the 'right' to emit at some known price. This works well in combination of emission constraints that have a hard ceiling. You can also make use of the Market object's ability to model a market price that varies according to demand so that the marginal cost of emissions increases as more generators demand the right to emit.

The Physical Contract class is designed to model contracts for generation or load that result in actual generation or load, as opposed to a purely financial contract.

In many ways Physical Contract is a simplified version of Generator and Purchaser rolled into one, although generally you use separate objects for generation and load contracts. The generation capacity or maximum load is set by Max Generation and Max Load properties respectively. You can define a multi-band generation offer or load bid using Offer Quantity, Offer Price or Bid Quantity, Bid Price. Minimum generation/load is set by Min Generation and Min Load.

The contracts can be owned by companies by defining Physical Contract Companies Share.

The selection of physical contracts can be optimized by the LT Plan capacity expansion plan: see Long Term Planning article for details.

This chapter briefly describes the features of the Company class. This class can be used to:

Collate solution data according to asset ownership;
Evaluate contract difference payments;
Provide portfolios definitions and settings for use in the PLEXOS models of imperfect competition

The Company class is a mechanism for collating solution data into logical groupings. For example, you might want to know the total revenues from a collection of generators owned by a company. You can create a Company object and add the company's Generator objects to that Company's Companies collection. The total pool revenues will then be reported, as well as other data, for the Company.

Four algorithms of imperfect competition are available. The simplest sets generator offers using a shadow pricing principle akin to Bertrand competition. The approach can be used separately or on combination with two medium-term equilibrium models that use either Nash-Cournot long-run marginal cost (LRMC) as drivers of generator markups. Finally PLEXOS implements the residual supply index (RSI) approach developed by the California ISO for its transmission economic assessment methodology (TEAM); an approach that has general application.

Company contract settlement is calculated from the Financial Contract properties Quantity, Cap Price and Floor Price. Alternatively the contract quantity can be a function of region load using the Financial Contract Region Load Participation Factor property, or generator load using the Financial Contract Generators Generation Participation Factor property.

The ownership relationship between companies and contracts is controlled by the property Financial Contract Generating Companies Share and a contract may be owned by multiple companies if required.

By default financial contracts are contracts-for-differences (CfD) and are settled at the regional energy price defined by the Financial Contract Region membership. This can be changed using the Region Pool Type attribute (gross or net) in combination with the Competition Contracts Hand-off Point to model a wider range of market contract styles.

Contract settlement changes the net profit of companies and therefore affects the medium term equilibrium models. They also affect the Nash-Cournot model by changing the total contract cover, which reduces the amount of capacity companies have for gaming.

Electricity market economics fall into the broad category of oligopoly economics. Oligopoly refers to a market structure that is more competitive than a monopoly, but less than 'perfect' competition. Several factors, not just the number for players, contribute to the degree of competitiveness in a market. For example, if there exists significant barriers to entry, such as high capital or financing costs, or regulation, the market will be less competitive, and the pricing outcome in the long run could be expected to reflect those entry costs, or the implied costs of those regulations. In the following we outline the methods available.

In the Bertrand theory of oligopoly, equilibrium is sought by price manipulation alone. In the simplest case of a dispatch by merit-order of costs, pseudo-Bertrand equilibrium is simple to find by raising each company's generator offer price to the level of a competitor next in the merit-order. This approach is straightforward to implement in an optimization framework and yields a solution that is a pseudo-equilibrium solution consistent with system constraints.

However, this simple shadow pricing strategy ignores the important effect of transmission congestion which can create pricing islands with less competition than the system as a whole. The attribute Competition Pricing Strategy controls the shadow pricing method and has three levels of increasing effect with respect to transmission congestion.

The weakness of the shadow pricing method is that it does not directly address the underlying costs of the entry to the market nor other fixed costs. Fixed operation and maintenance costs, capital and debt costs imply and underlying long-run marginal cost (LRMC) that must be recovered by generators from the market. The medium term equilibrium models in PLEXOS attempt to address this issue.

In the theory of Nash-Cournot equilibrium players manipulate the quantity offered to the market under the assumption that there is some price elasticity of demand i.e. that the price the customers are prepared to pay for supply goes up as supply is withdrawn and vice versa. The objective then is for the Cournot players to maximise profits, taking into account the reaction of other players in the market.

This method has its difficulties in that it does not directly address the underlying costs of the industry (like cost of investment), rather it seeks 'simply' to maximise profits of a small number of players. Crucially it makes the assumption of price elasticity of demand, and in an electricity market there is virtually none with the timeframe of a single dispatch interval. Thus a pure Nash-Cournot method is not particularly suited to modelling electricity markets. However, the method developed for PLEXOS draws on the strengths of the method by solving the equilibrium only in the medium term and 'decomposing' that medium term equilibrium into mark-ups that can be meaningfully applied to the short time frames of the real market.

The setting Competition Equilibrium Model switches the Nash-Cournot model 'on'. You must run MT Schedule with this even if you are also running ST Schedule. There is a default elasticity set by the Competition Default Elasticity. This elasticity is the change on an annual basis in demand in response to price; however it does not affect the actual input loads; they remain as input, with only the mark-up strategy of players affected by the elasticity.

NOTE:
If you need to set the elasticity by Region use Cournot objects.

In most situations, the energy prices calculated by the market will be sufficient to compensate generators for their variable costs. There are other dispatch-related costs e.g. start costs and no load costs that will not necessarily be recovered by marginal cost based pricing, and some constraints can force prices below SRMC. But even if prices are sufficient to recover variable costs, it is unlikely that they will cover fixed operations and maintenance, capital cost, and debt cost.

The simulator can set generator mark-ups to achieve revenues on a company basis sufficient to recover all fixed costs from the market or more precisely so that companies at least break even over an annual timeframe when all fixed costs are considered.

Generator and Transmission Line Fixed Costs

These fixed costs are entered as properties on Generator and Line objects with the FO&M Charge, Equity Charge and Debt Charge in units of $/kW/year. Together, these properties define a fixed cost charge that portfolios (Companies) must recover from the market.

Fixed costs are reported in aggregate on the Generator, Line and Company and also by Region. Because they are annual charges the Generator Fixed Costs reporting is done down to the interval level the simulator must allocate the fixed costs to intervals. This is done in two stages, firstly by MT Schedule down to the LDC block level, and then by ST Schedule down to the interval. The allocation is in proportion to Pool Revenue (for Generator) or Rental (for Line) earned; the higher the earnings, the higher the fixed cost allocation. This step is important because it determines what fraction of the annual fixed cost should be recovered in each step.

NOTE

In order to be involved in LRMC recovery generators and lines must belong to company objects

LRMC Recovery Method

The LRMC recovery method is described in the article LRMC Recovery Algorithm. The source code is provided as a code sample with every installation. The algorithm is turned on by the attribute Competition Equilibrium Model. Like the Nash-Cournot it requires that MT Schedule is enabled even if you are running ST Schedule. There are two algorithmic options for LRMC recovery.

The Company property Strategic can be used to control the extent to which a company can 'game' the market. The property can be set to a value between zero and 100% with 100% as the default. The value represents the proportion of the company generation that is available for gaming. For example, if a company produced 6000 GWh under in the perfect competition outcome and Strategic is set to 30% then (1-0.3) × 6000 = 4200 GWh will be held out of the game. This is done by adding constraints on total company generation such that, no matter what mark-ups they apply they will always generate this percentage of perfect competition output.

Setting Strategic to zero is a special case. It causes the Company to be excluded from the LRMC recovery i.e. they act as a price taker.

The Company property Mark-up Bias changes the bias towards peak revenue periods with higher values pushing more mark-up into peak periods.

With the flexibility of the Strategic property it is possible to perform market power studies of individual companies or groups of companies. Further, by adjusting the total fixed cost requirements, it is possible to measure the ability of a company or set of companies to maximize profits. This is useful for merger studies where the ability of a portfolio to influence market prices without losing volume can be measured in the 'before' and 'after' merger cases.

Please refer to the article Residual Supply Index.

This chapter describes the features of the constraint class. The general form of a constraint is:

∑( j )( ai,j' xj {≤, =, ≥} b

where:

ai,j is a constant (left-hand side coefficient)
xj is a variable in the formulation
bi is a constant (right-hand side)

Constraints are used in a wide range of applications. For example when modelling transmission networks they can be used to approximate voltage and stability limits that are not included in the linearized DC load flow used. In an operational setting they can be used to model complex dependencies between units, for example that one unit cannot run unless another is running. In capacity expansion planning they are used to model project dependencies like project timing constraints.

NOTE This facility is extremely powerful and easily extensible. If you require aspects of the system to be subject to the constraints for your problem that do not appear in the current version, do not hesitate to request this to be expanded.

The Constraint class allows you to define generic constraints involving a wide range of variables and constants in the PLEXOS power system mathematical formulation. This facility is the principle mechanism for defining custom transmission, generation, fuel, emission and other constraints.

The Constraint attribute Sense sets the constraint type or direction: less-than-or-equal-to (value -1), equal-to (value 0), or greater-than-or-equal-to (value 1).

The property RHS and its variants by hour, day, week, month, year and custom sets the right-hand side value which is the constant part of the constraint: all coefficients are defined on the left-hand side of the constraint. Which version of RHS is used determines the scope of the constraint e.g. if you use RHS Month then there will be one constraint per day. The RHS values can be patterned and dated as with any other property.

Constraint objects have several collections whose members determine what exactly is subject to constraint. There are no default variables that are constrained when objects are added to the constraint so you must define the left-hand side coefficient values.

Example: Generic constraint involving a generator and a line

Membership	Property	Value	Units
Constraint (Voltage Limit)	Sense	>=	-
Constraint (Voltage Limit)	RHS	0	-
Generator.Constraints(CT1)	Generation Coefficient	1	-
Line.Constraints (A-B)	Flow Forward Coefficient	-0.2	-

PLEXOS includes an automatic feasibility repair algorithm which detects and fixes infeasibilities in user-defined generic constraints. Check the log files of your model runs for infeasibility messages. If you see these messages then scan the list of implicated constraints for "Con_x" where x is the name of your Constraint. If it is consistently violated and requiring repair it is best to allow the violations at a price using a penalty function.

By default generic constraints are 'hard' constraints. If they must be violated they will cause infeasibilities in the mathematical programming problem. For efficiency reasons, if you are certain that the constraint will never generate an infeasibility then it is best to leave it to be modelled as a 'hard' constraint.

However there are many situations in which constraint violations could and should be allowed. The Constraint Penalty Quantity and Penalty Price properties allow you to set up a multi-band penalty function. If only one level of penalty is required then simply setting the Constraint Penalty Price will ensure that any violations are priced at that level. Any number of violation bands can be specified using Penalty Quantity, and Penalty Price with increasing Band number. The lowest priced bands will be chosen first.

Constraint activity, violation, and pricing are reported in the solution database.

This guide describes modelling with complex calculated right-hand side expressions

Introduction

A PLEXOS Constraint object defines a set of constraints that appear in the mathematical programming problem. Constraints are of the general form:

∑ left-hand side terms {≤,=.≥} right-hand side constant

Depending on the period type of the right-hand side property, a single Constraint object can generate one or multiple constraints in the formulation e.g. [RHS] defines one constraint for each interval of the simulation while [RHS Week] defines one for each week.

A variety of left-hand side terms are available through the collections on the Constraint class e.g. to set a left-hand side coefficient for a line flow, set Constraint Lines [Flow Coefficient]. A Constraint may include any number of left-hand side terms, but is restricted to a single right-hand side constant. As with most properties, the right-hand side may vary over time (Date From, Date To, Timeslice), or stochastically according to a Variable, but for any one constraint in the formulation the right-hand side is usually constant.

However, modelling applications exist in which the right-hand side is defined by an equation and is not a simple constant. For example, transmission flow limits that depend on a complex combination of factors such as system inertia. This is where the Constraint RHS Constant feature comes in. It enables complex expressions on the right-hand side that will be evaluated iteratively during the simulation.

Working with the Feature

The "RHS Constant" (expressions) feature is available as a property on the constraint itself. This property is unique in that its value is not used and the expression itself needs to be entered into the "Expression" field, i.e. this property needs to be dynamic.

Please note that the Constraint RHS property must also be defined. The evaluated RHS Constant value is added to the RHS value (which can of course be zero).

RHS Constant can be tagged with a date ('Date From' and/or 'Date To'), a timeslice or a scenario. However, as stated the value itself is ignored, therefore the value and data file fields will be omitted if any values have been entered.

Figure 1: RHS Constant definition for a Constraint

The expression field will accept plain text of any length. It can accept multi-line text, and this is convenient for the readability of the expressions. To type multi-line text use SHIFT-Enter to create new lines while typing. To paste multi-line data, the text must be delimited by quotes. Pasting from a multi-line Excel worksheet cell will preserve the multi-line text.

Expression Syntax

RHS_CONSTANT text expressions are composed of 'tokens', separated by spaces or new lines, and are of two types:

Operators: listed in the table below, and
Operands: either numbers or references to variables in the formulation as explained below.

Tokens are organised in the expression according to Reverse Polish notation (RPN). This is a mathematical notation in which operators follow their operands (e.g. a b +), in contrast to Polish notation (PN), in which operators precede their operands (a + b). It does not need any parentheses if each operator has a fixed number of operands.

Example:

Polish notation: a × (b + c) - d

Reverse Polish notation: a b c + × d -

RPN is preferred for processing by computer code. It makes use of a 'stack' (memory) to keep track of operands and processes operators as they are encountered. A stack is a last-in-first-out (LIFO) queue. Items can be pushed onto the stack (in which case the new item becomes the top stack element) or popped off the stack (where the top stack element pops first).

The stack operations for the above example are as follows:

Token "a"	push "a" on the stack
Token "b"	push "b" on the stack - it is now composed to two elements with "b" as the top element
Token "c"	push "c" on the stack - it is now composed of three elements with "c" on top
Token "+"	pop "c" and "b" from the stack, add them and return the result to the stack - it now has two elements with c+b on top
Token "×"	pop c+b and a from the stack, multiply and return the result to the stack - it now has a single element being a×(b+c)
Token "d"	push "d" on the stack
Token "-"	pop "d" and a×(b+c) from the stack, subtract and return the result to the stack

The 'result' is read off the top of the stack which is a × (b + c) - d.

Note that when processing RHS_CONSTANT the stack is automatically initialized with one element (0) at the top of the stack.

The supported operators are in Table 1. All the examples shown result in the top stack element ('the result') being 1000.

Table 1: RPN operators

Operator	Name	Operands	Net Stack Effect	Function	Example
ABS	Absolute Value	1	0	Pops the top element of the stack takes its absolute value and pushes the result to the top of the stack	"-1000 ABS ADD"
ADD	Addition	2	-1	Pops and adds the top two elements of the stack and pushes the result to the top of the stack	"800 200 ADD ADD"
DIV	Division	2	-1	Pops and divides the top two elements of the stack and pushes the result to the top of the stack. The denominator is the top stack element, the numerator the second element.	"2000 2 DIV ADD"
DUP	Duplicate	1	1	Increases the stack height by one by duplicating the value of the top stack element	"500 DUP ADD ADD"
MAX	Maximum	2	-1	Pops and takes the maximum of the top two stack elements and pushes the result to the top of the stack	"100 900 EXCH ADD ADD"
MIN	Minimum	2	-1	Pops and takes the minimum of the top two stack elements and pushes the result to the top of the stack	"1000 500 0 POP EXLEZ EXCH POP ADD"
MUL	Multiply	2	-1	Pops and multiplies the top two elements of the stack and pushes the result to the top of the stack	"450 1000 MAX ADD"
NEG	Negation	1	0	Pops the top element of the stack reverses its sign and pushes the result to the top of the stack	"1000 1100 MIN ADD"
POP	Pop	1	-1	Pops the top stack element, and if the value is less than or equal to zero sets the flag for the EXLEZ operator to true	"10 100 MUL ADD"
RSD	Roll Stack Down		0	Moves the top element of the stack to the second to bottom position	"-1000 NEG ADD"
RSU	Roll Stack Up		0	Moves the second to bottom element of the stack to the top	"31.62 POW2 ADD"
SUB	Subtract	2	-1	Pops and subtracts the first element from the second and pushes the result to the top of the stack	"10 POW3 ADD"
EXCH	Exchange	2	0	Exchanges the top two stack elements	"2 2000 0 RSD ADD DIV ADD"
POW2	Square	2	-1	Pops and squares the top elements of the stack and pushes the result to the top of the stack.	"2 0 2000 RSU ADD DIV ADD"
POW3	Cube	2	-1	Pops and cubes the top elements of the stack and pushes the result to the top of the stack.	"1000000 SQRT ADD"
STEP S	Step function	1	0	Pops the top element of the stack and pushes 1 if the value is greater than zero otherwise 0 and pushes the result to the top of the stack	"1000 GenLoad_A.1 STEP MUL ADD"
SQRT	Square root	1	0	Pops and takes the square root the top elements of the stack and pushes the result to the top of the stack.	"1500 500 SUB ADD"
EXLEZ	Exchange if less than or equal to zero	2	0	If the POP operator last returned true the EXCH command is performed on the stack	"-1000 ABS ADD"

Variable References as Operands

Expressions may include references to the solution values of variables in the formulation. For example, you may want to refer to the output of a generator. The reference must exactly match the name of the variable in the formulation and if the name includes spaces you must enclose the references in quotes. Variable names have two parts:

The prefix: which describes why type of variable it is, and
The name: which matches the name of the object in the input database.

Most variables can be referenced, and some example references are described in Table 2. The only restriction is that the variable being referenced must have the same indices as the constraint i.e. the constraints are indexed by simulation period and so any referenced variable must also be indexed by simulation period.

Table 2: Example formulation variable references

Property	Reference type	Prefix	Object name	RPN token	Notes
Generator load	Formulation	GenLoad_	GenA	GenLoad_GenA	Formulation variables shown in LP files
Generator load	Formulation	GenLoad_	Gen 10	"GenLoad_Gen 10"	Whitespace in object name, hence ""
Line Flow	Formulation	LinFlow_	A-B	LinFlow_A-B	Transmission example
Battery charging	Formulation	BatChrg__	BESS1	BatChrg__BESS1	Note the prefix has two underscores
Battery discharging	Formulation	BatDChg__	BESS1	BatDChg__BESS1	Note the prefix has two underscores

If you need a value which is not available as a native formulation variable (i.e. within an LP file), its value can be supplied by:

Defining and referencing a Variable (if the quantity is fixed before the simulation begins). Use with Formulate Value.
Defining and referencing a Decision Variable (if the value is subject to co-optimisation and not known before simulation commencement).

By default, both Variables and Decision Variables values are automatically lagged by one time period. The right-hand side for a constraint in time period t will be computed from variable values for period t-1. However there may be some variables which do not need to be lagged, for example load related variables, where the load values are from a known profile. In this case '{0}' can be appended to the RPN token, specifying there is no lag applied to the variable value reference. The default lag for both variables and decision variables can be disabled in this way.

Table 3: Example variable and decision variable references

Property	Reference type	Prefix	Object name	RPN token	Notes
Decision Variable Value	Decision Variable	Var_	OpMode	Var_OpMode	Default 1-period lag applies
Decision Variable Value	Decision Variable	Var_	OpMode	Var_OpMode{0}	No lag
Decision Variable Value	Decision Variable	Var_	Region A Load	"Var_Region A Load"	Whitespace in object name
Variable Value	Variable	VarValue_	LoadGrowth	VarValue_LoadGrowth	Use with Formulate Value, 1-period lag
Variable Value	Variable	VarValue_	LoadGrowth	VarValue_LoadGrowth{0}	Use with Formulate Value, no lag

Examples:

Consider a transmission line limit that is set by taking the minimum of two calculated values according to the formulae:

MIN
(1.983 * (Var_Y -0.4992 * (0.0259 * Var_LOAD{0} + 11.69) + 1.32 - 10),
1.725 * (Var_X -0.7426 * (0.0259 * Var_LOAD{0} + 11.69) + 0.07139 - 10)))

Here Var_Y , Var_X and Var_LOAD refer to Decision Variable objects ("Var_" being the prefix for Decision Variable and the remainder being the name of the objects).

The RPN for this is:

"Var_X
-0.7426 0.0259 Var_LOAD{0} MUL 11.69 ADD MUL ADD
0.07139 ADD
-10 ADD
1.725 MUL
Var_Y
-0.4992 0.0259 Var_LOAD{0} MUL 11.69 ADD MUL ADD
1.32 ADD
-10 ADD
1.983 MUL
MIN"

For illustration, assume the decision variable references take these values:

Var_X = 137
Var_LOAD = 1414.09702044226
Var_Y = 141

The stack operations for this expression are as follows:

(Token: Var_X)	Push 137
(Token: -0.7426)	Push -0.7426
(Token: 0.0259)	Push 0.0259
(Token: Var_LOAD)	Push 1414.09702044226
(Token: MUL)	Pop 1414.09702044226	Push 36.6251128294545
(Token: 11.69)	Push 11.69
(Token: ADD)	Pop 11.69	Push 48.3151128294545
(Token: MUL)	Pop 48.3151128294545	Push -35.8788027871529
(Token: ADD)	Pop -35.8788027871529	Push 101.121197212847
(Token: 0.07139)	Push 0.07139
(Token: ADD)	Pop 0.07139	Push 101.192587212847
(Token: -10)	Push -10
(Token: ADD)	Pop -10	Push 91.1925872128471
(Token: 1.725)	Push 1.725
(Token: MUL)	Pop 1.725	Push 157.307212942161
(Token: Var_Y)	Push 141
(Token: -0.4992)	Push -0.4992
(Token: 0.0259)	Push 0.0259
(Token: Var_LOAD)	Push 1414.09702044226
(Token: MUL)	Pop 1414.09702044226	Push 36.6251128294545
(Token: 11.69)	Push 11.69
(Token: ADD)	Pop 11.69	Push 48.3151128294545
(Token: MUL)	Pop 48.3151128294545	Push -24.1189043244637
(Token: ADD)	Pop -24.1189043244637	Push 116.881095675536
(Token: 1.32)	Push 1.32
(Token: ADD)	Pop 1.32	Push 118.201095675536
(Token: -10)	Push -10
(Token: ADD)	Pop -10	Push 108.201095675536
(Token: 1.983)	Push 1.983
(Token: MUL)	Pop 1.983	Push 214.562772724588
(Token: MIN)	Pop 214.562772724588	Push 157.307212942161
Result = 157.307212942161

Sub expressions

A complex expression that is shared between multiple Constraint right-hand side expressions can be defined using a Decision Variable/Constraint pair and referred to using the "Var_" prefix in your RHS_CONSTANT expressions. To do this, follow these steps:

Create a Decision Variable with [Objective Function Value] = 0.0 e.g. Decision Variable "INERTIA"
Create a Constraint of the same name with [RHS] = 0.0 e.g. Constraint "INERTIA"
Create a membership that puts the Constraint in the Decision Variable's [Definition] collection.
Define the RHS_CONSTANT on the new Constraint like the following example

Decision Variable "INERTIA" RHS_CONSTANT:

"5.26 GenLoad_OCGT3 STEP MUL ADD
5.26 GenLoad_OCGT2 STEP MUL ADD
5.26 GenLoad_OCGT1 STEP MUL ADD
0.02891 GenLoad_OCGT4 MUL ADD
0.89 GenLoad_OCGT5 STEP MUL ADD
0.89 GenLoad_OCGT6 STEP MUL ADD
7.89 GenLoad_OCGT7 STEP MUL ADD
14.61 GenLoad_OCGT8 STEP MUL ADD
31.4 GenLoad_CCGT STEP MUL ADD
GenLoad_CCGT -237 ADD STEP 16.29 MUL ADD
0.0362 GenLoad_OCGT9 MUL ADD
2.09 GenLoad_OCGT10 STEP MUL ADD
0.89 GenLoad_OCGT11 STEP MUL ADD
0.89 GenLoad_OCGT12 STEP MUL ADD
0.89 GenLoad_OCGT13 STEP MUL ADD
0.89 GenLoad_OCGT14 STEP MUL ADD
10.065 GenLoad_OCGT15 STEP MUL ADD
0.02 GenLoad_OCGT16 MUL ADD
7.95 GenLoad_STA1 STEP MUL ADD
7.95 GenLoad_STA2 STEP MUL ADD
7.95 GenLoad_STA3 STEP MUL ADD
7.95 GenLoad_STA4 STEP MUL ADD
9 GenLoad_STB1 STEP MUL ADD
9 GenLoad_STB2 STEP MUL ADD
9 GenLoad_STB3 STEP MUL ADD
9 GenLoad_STB4 STEP MUL ADD
0.52 GenLoad_OCGT18 STEP MUL ADD
0.014 GenLoad_OCGT17 MUL ADD"

You can now use this expression in other RHS_CONSTANT expressions by referring to its name e.g. "Var_ INERTIA" as in the following example for Constraint "ROCOF":

"1
3
100 Var_INERTIA MUL ADD
0.04 MUL MUL ADD
1
3
100 Var_INERTIA MUL ADD
0.04 MUL
24 ADD MUL
1
1 STEP MUL
POP
EXLEZ
EXCH POP"

Flow of Execution

Constraints that define RHS_CONSTANT are enforced iteratively along with other similar constraints (such as transmission constraints) during the simulation process. An iterative approach is used, first solving with no constraints in the formulation, then checking for violations by computing the current value of the right-hand side (based on the result of the expression plus any input right-hand side part) and adding constraints if violations are detected and repeating until all constraints are enforced and no right-hand side values require further updating.

Convergence

Right-hand side constants based on complex expressions can result in a different convergence process than regular constraints i.e. those with fixed right-hand side values. With regular constraints, the addition of new limits increases the objective function value every iteration and convergence is achieved as soon as either:

no more constraints are violated, or
the problem is infeasible.

In particular, it is constraint right-hand side expressions that include integer switches (such as the STEP, MIN, MAX operators) can lead to situations where the simulation cycles between solutions or fails to fully converge after many iterations.

The simulation program detects when cycling is occurring according to the following rules:

If an iteration returns an objective value equal to any previous iteration, the iterations are stopped (as in Figure 3).
If the absolute value of the change in objective function between iterations begins to increase (rather than decreasing as expected in a linear system) the iterations can continue until the next time the objective function ticks up and which point the iterations are stopped (Figure 4).

Figure 3: Convergence

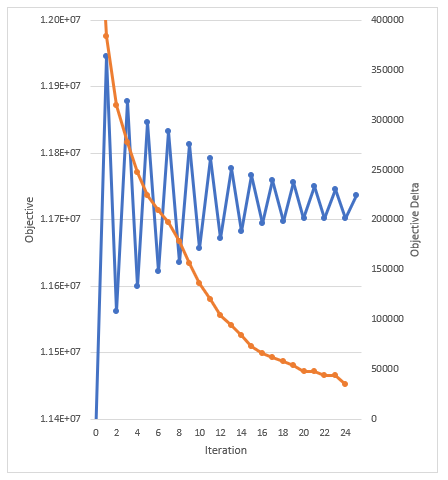
Figure 4: Nonconvergence due to cycling

Progress Messages and Reporting

There are two Diagnostic switches that apply to constraint iterations as highlighted in Figure 5. The option [Monitored Iterations Summary] prints a one-line summary at the conclusion of constraint convergence, whereas [Monitored Iterations] prints messages for each iteration as in the following example:

Figure 5

Here "columns" is the number of new variables added, "rows" the number of new constraints and "rhs" is the number of previously-added constraint right-hand side values updated in the iteration. "Obj" is the objective function value.

The Decision Variable class creates user-defined variables in the mathematical programming formulation. These variables can be used for a wide variety of modelling purposes including:

Modeling commodities with a demand such as desalination as a product of electric power and heat.
Modeling the storage electricity or any other commodity.
Calculating values that are functions of intrinsic decision variables and passing these to the solution.
Cancelling out default objective function coefficients by defining a decision variable to be equal to an intrinsic variable with the opposite objective function term.
Enforcing integer restrictions on decision variables that are intrinsically linear.
Modeling piecewise or general non-convex or discontinuous functions.

To key property for Decision Variable is Objective Function Coefficient although you may simply set this to zero if desired. Other important properties are Lower Bound and Upper Bound and Type (linear or integer).

Once the variable is defined you may use it in Constraint objects or 'inject' the variable into the built-in formulation.

Concise Modelling Guide

Contents

1. Introduction

2. Intended Function

3. How PLEXOS Works

3.1. Data Storage

3.2. Object Model

3.3. Collections and Properties

3.4. Configuration

3.5. Simulation Engine

3.6. Capacity Expansion Planning

3.7. Capacity Adequacy and Maintenance Planning

Discrete maintenance

Distributed maintenance

Forced outage

3.8. Medium- term scheduling and simulation

3.9. Short-term Scheduling and Simulation

3.10. Stochastic Variables

3.11. Models of Imperfect Competition

3.12 Solver engines

3.13. Output

3.14. Program Architecture

3.15. Object Model

4. Load and Transmission

4.1. Load

4.2. Transmission Network

5. Generators

5.1. Creating a Generator

5.2. Generator Injection Point

5.3. Station Auxiliaries and Loss Factors

5.4. Fuel Use and Constraints

5.5. Unit Heat Rate

5.6. Offers

5.7. Mark-up

5.8. Unit Commitment

5.9. Must-run, Energy and Other Constraints

5.10. Fuel Contracts

5.11. Forced Outage and Maintenance

5.12. Fixed Costs

5.13. Combined Cycle Gas Turbine (CCGT)

5.14. Combined Heat and Power (CHP)

5.15. Hydro and Pumped Storage

5.16. Synchronous Condenser Operation

5.17. Capacity Expansion

6. Reserves/ Ancillary Services

6.1. Type and Timeframe

Raise

Lower

Regulation Raise

Regulation Lower

Replacement

Operational

6.2. Reserve Requirement

6.3. Generator Reserve Provision

6.4. Reserve Dispatch and Pricing

6.5. Interruptible Load

6.6. Offers for reserve provision

7. Emissions

7.1. Emission Objects

7.2. Fuel Emissions

7.3. Generator Emissions

7.4. Emission Removal

7.5. Abatement Devices

7.6. Dispatch and Account Prices

7.7. Emission Constraint

7.8. Emissions Market

8. Physical Contracts

9. Companies, Financial Contracts and Imperfect Competition

9.1. Contract Position

9.2.Models of oligopoly

9.3. Shadow Pricing (Bertrand)

9.4. Nash-Cournot Equilibrium

9.5. LRMC Recovery

9.6. Controlling Companies Behaviour

9.7. Residual Supply Index

10. Generic Constraints

10.1. Constraint Objects

10.2. Constraint Coefficients

10.3. Feasibility Repair

10.4. Constraint Violation